



Next: B.2 Rectangular Patterns
Up: B. Analytical Fourier Transformations
Previous: B. Analytical Fourier Transformations
B.1 Triangular Patterns
An arbitrary triangle consisting of three points
{(x1, y1),(x2, y2),(x3, y3)} in
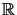 2 can always be
transformed to the unit triangle
{(0, 0),(1, 0),(0, 1)} by
2 can always be
transformed to the unit triangle
{(0, 0),(1, 0),(0, 1)} by
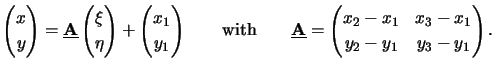 |
(B.2) |
The module of the determinant of the transformation matrix
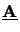 equals
equals
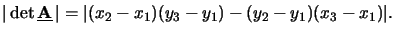 |
(B.3) |
Using (B.2), the integral (B.1) writes
for triangular patterns to
whereby TRI-1 refers to the unit triangle
and the coefficients
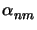 ,
,
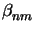 and
and
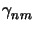 are
given by
The function
I
are
given by
The function
I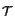 (
(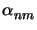 ,
,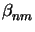 ) is calculated as
follows:a
) is calculated as
follows:a
![$\displaystyle I_{\mathcal{T}}(\alpha_{nm},\beta_{nm}) = \begin{cases}\displayst...
...a_{nm}-\alpha_{nm}} e^{-j\pi\beta_{nm}} \right] & \text{otherwise.} \end{cases}$](img1471.gif) |
(B.5) |
Footnotes
- ...
follows:a
- The function
si(x) is defined as
si(x)
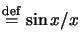 .
.




Next: B.2 Rectangular Patterns
Up: B. Analytical Fourier Transformations
Previous: B. Analytical Fourier Transformations
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
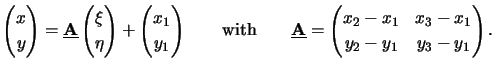
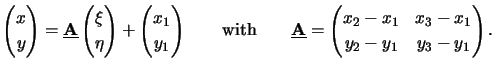
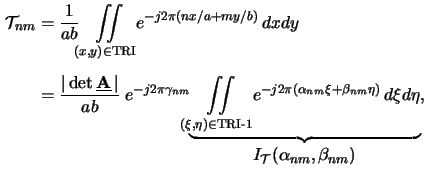
![$\displaystyle I_{\mathcal{T}}(\alpha_{nm},\beta_{nm}) = \begin{cases}\displayst...
...a_{nm}-\alpha_{nm}} e^{-j\pi\beta_{nm}} \right] & \text{otherwise.} \end{cases}$](img1471.gif)