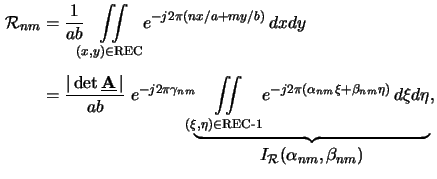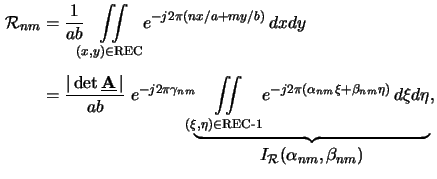Next: B.3 Numerical Evaluation
Up: B. Analytical Fourier Transformations
Previous: B.1 Triangular Patterns
B.2 Rectangular Patterns
Similarly a general rectangle
{(x1, y1),(x2, y2),(x3, y3),(x4, y4)}
in
 2 can always be transformed to the unit rectangle
{(0, 0),(1, 0),(0, 1),(1, 1)} by the transformation (B.2).
For rectangular patterns the integral in (B.1) equals to
whereby REC-1 refers now to the unit rectangle and
the coefficients
2 can always be transformed to the unit rectangle
{(0, 0),(1, 0),(0, 1),(1, 1)} by the transformation (B.2).
For rectangular patterns the integral in (B.1) equals to
whereby REC-1 refers now to the unit rectangle and
the coefficients
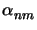 ,
,
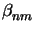 and
and
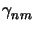 are given by (B.5) again. The function
I
are given by (B.5) again. The function
I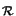 (
(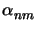 ,
,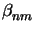 ) is calculated to
) is calculated to
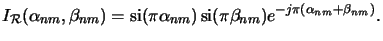 |
(B.6) |
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17