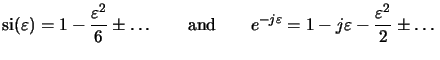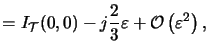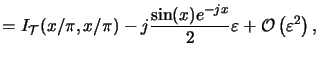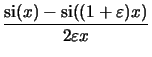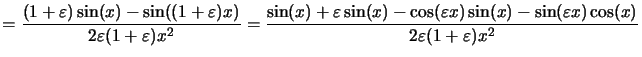Next: C. Stratified Medium
Up: B. Analytical Fourier Transformations
Previous: B.2 Rectangular Patterns
B.3 Numerical Evaluation
In Section 4.4.1 it is shown that aliasing errors are
avoided by the analytical transformation of the mask transfer function.
Although aliasing is suppressed, the numerical evaluation of the provided
analytical formulae (B.6) and (B.8)
can introduce errors due to the finite machine precision.
Special care has to be taken for
si(x) = sin(x)/x since
it is an indefinite expression for
x  0. In (B.6)
cancellation errors can occur due to the required subtractions. The
following perturbation analysis proves that both formulae (B.6)
and (B.8) are numerically robust and stable.
Consequently the proposed semi-analytical algorithm for
the calculation of the Fourier coefficients of the mask transmission function
neither lacks aliasing nor numerical evaluation errors.
0. In (B.6)
cancellation errors can occur due to the required subtractions. The
following perturbation analysis proves that both formulae (B.6)
and (B.8) are numerically robust and stable.
Consequently the proposed semi-analytical algorithm for
the calculation of the Fourier coefficients of the mask transmission function
neither lacks aliasing nor numerical evaluation errors.
The Taylor series expansions of the two functions
si(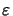 ) and
exp(- j
) and
exp(- j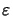 )
for
|
)
for
|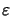 |
| 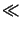 1, i.e.,
1, i.e.,
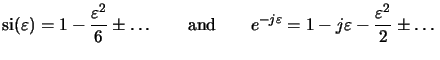 |
(B.7) |
readily show that the formula
I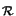 (
(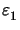 /
/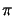 ,
,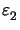 /
/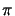 )
in (B.8) valid for rectangular patterns is stable for
|
)
in (B.8) valid for rectangular patterns is stable for
|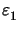 |,|
|,|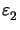 |
| 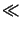 1 since
1 since
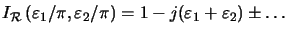 |
(B.8) |
For triangular patterns the evaluation of the second and third cases
in (B.6) is particularly peculiar since
cancellation errors are potentially caused by the required subtractions.
The two cases are studied separately
by inserting the Taylor expansions (B.9) into (B.6)
and linearizing the expressions:
- Case II in (B.6):
- Case III in (B.6):b
Summarizing (B.10) to (B.12),c
proves the robustness of all formulae. In the actual implementation these
Taylor expansions are used to avoid numerical instabilities.
Footnotes
- ...):b
- Using Taylor expansions for
cos(
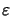 x) = 1 -
x) = 1 - 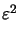 x2/2
x2/2 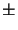 ... and
sin(
... and
sin(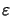 x) =
x) = 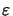 x
x  ...
yields:
...
yields:
- ...),c
- Note
that in (B.12) the first term equals the expression for the
second case in (B.6) since
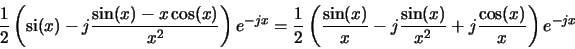
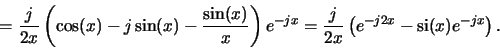




Next: C. Stratified Medium
Up: B. Analytical Fourier Transformations
Previous: B.2 Rectangular Patterns
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
![]() ) and
exp(- j
) and
exp(- j![]() )
for
|
)
for
|![]() |
| ![]() 1, i.e.,
1, i.e.,