Matrix Notation

We introduce now a compact matrix notation for the two relations (C.5) and (C.7) by combining them like

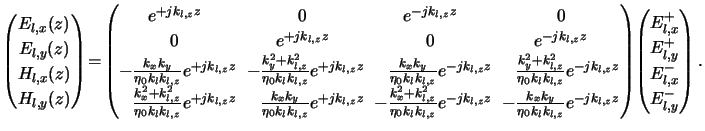
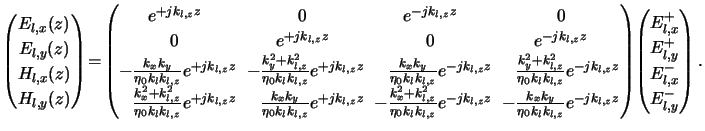$$\begin{pmatrix}E_{l,x}(z)\\ E_{l,y}(z)\\ H_{l,x}(z)\\ H_{l,y}(z) ... ...x}\!\begin{pmatrix}E^+_{l,x}\\ E^+_{l,y}\\ E^-_{l,x}\\ E^-_{l,y} \end{pmatrix}.$$ (C.6)

Summarizing the z-dependent part of the lateral components of the electric and magnetic field in u_l(z) and, similarly, the electric amplitudes propagating upwards and downwards the layer in e_l, i.e.,

 

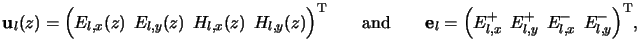$$\mathbf{u}_l(z) = \Big( E_{l,x}(z)\;\,E_{l,y}(z)\;\,H_{l,x}(z)\;\... ..._l = \Big( E^+_{l,x}\;\,E^+_{l,y}\;\,E^-_{l,x}\;\,E^-_{l,y} \Big)^{\mathrm{T}},$$ (C.7)

we simply obtain

 

$$\mathbf{u}_l(z) = \underline{\mathbf{C}}_l(z)\,\mathbf{e}_l.$$ (C.8)

The matrix $\underline{\mathbf{C}}_{l}^{}$(z) definitely describes the field propagation in the layer l, i.e., the electric and magnetic field can be calculated at any vertical position z within the layer from the above equation (C.10).