



Next: Bibliography
Up: PhD Thesis Heinrich Kirchauer
Previous: C.2 Stack of Homogeneous
D. Nonplanar Material Interface
The error introduced by the truncation (6.27) of
the Fourier expansion of the EM field is now investigated for the
stepped topography of Figure 8.16. A sketch of the
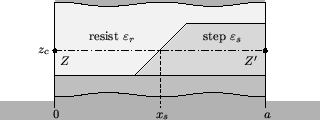
relevant region of the geometry is re-plotted in Figure D.1.
All derivations are performed in two dimensions only since the results apply
to three dimensions as well.
Figure D.1:
Schematic of the investigated nonplanar material interface (left)
and lateral dependence of the permittivity along a horizontal cut
 (right). The cut positions Z and Z
(right). The cut positions Z and Z are
chosen within the nonplanar region of the resist.
are
chosen within the nonplanar region of the resist.
|
|
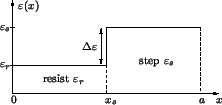
The lateral dependence
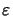 (x) of the permittivity is simply given by
(cf. Figure D.1)
(x) of the permittivity is simply given by
(cf. Figure D.1)
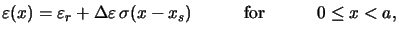 |
(D.1) |
with
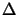
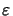 =
= 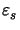 -
- 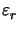 as the difference of the resist and step material
permittivities. The intersection
of the cut-line
as the difference of the resist and step material
permittivities. The intersection
of the cut-line
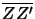 with the step slope is denoted by xs,
and
with the step slope is denoted by xs,
and 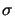 (x) refers to Heaviside's step function.a
The differential method requires the Fourier coefficients
(x) refers to Heaviside's step function.a
The differential method requires the Fourier coefficients
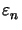 of the
permittivity function
of the
permittivity function
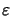 (x) of (D.1),
(x) of (D.1),
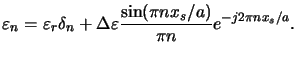 |
(D.2) |
We restrict our investigations to TE-polarized light. In this case
the Fourier coefficients
Ey, n(z) of the y-component of the electric field
satisfyb
![$\displaystyle \frac{d^2 E_{y,n}(z)}{dz^2} = \sum_{m}\left[k_{x,n}^2\delta_{nm}-k_0^2\varepsilon_{n-m}(z)\right]E_{y,m}(z).$](img1654.gif) |
(D.3) |
The impact of the truncation of the Fourier series can best be understood
by explicitly studying one specific mode
Ey, i(z) at an
arbitrary vertical cut-position zc, e.g., at
 as indicated in Figure D.1. For the analysis the amplitude of
Ey, i(zc) can be chosen arbitrarily.
We conveniently set it equal to 1/k02 so that
as indicated in Figure D.1. For the analysis the amplitude of
Ey, i(zc) can be chosen arbitrarily.
We conveniently set it equal to 1/k02 so that
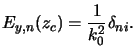 |
(D.4) |
Inserting this relation into (D.3) gives
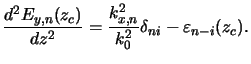 |
(D.5) |
For simplicity we consider only the case when
kx, n2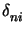 vanishes,
i.e., the propagation of the vertical mode i = 0 or, equivalently, the energy
spread of an arbitrary order i into the zeroth-order n = 0 is studied. Since
the vertical propagating mode usually carries most of the energy, this
restriction gives still valuable information.
vanishes,
i.e., the propagation of the vertical mode i = 0 or, equivalently, the energy
spread of an arbitrary order i into the zeroth-order n = 0 is studied. Since
the vertical propagating mode usually carries most of the energy, this
restriction gives still valuable information.
The impact of the truncation of the Fourier expansions (6.27)
is now quantified by the following measure
describing the ratio between ``lost'' and ``total'' energy spread:
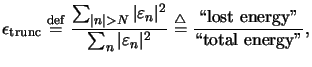 |
(D.6) |
This quantity
 can be interpreted as truncation
error since it describes the error made in the calculation of the second
derivative (cf. (D.5)).
Note that the measure is restricted to n = 0 or i = 0 since only then
the first term
kx, n
can be interpreted as truncation
error since it describes the error made in the calculation of the second
derivative (cf. (D.5)).
Note that the measure is restricted to n = 0 or i = 0 since only then
the first term
kx, n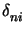 vanishes in (D.5).
The extension to the general situation is self-evident.
vanishes in (D.5).
The extension to the general situation is self-evident.
We will now derive an upper bound for
 .
For that we first evaluate the denominator occurring
in (D.6) with the
help of Parseval's theorem [131, p. 224] to (cf. (D.1))
.
For that we first evaluate the denominator occurring
in (D.6) with the
help of Parseval's theorem [131, p. 224] to (cf. (D.1))
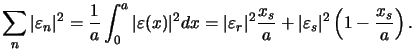 |
(D.7) |
Next we consider the numerator of (D.6).
An upper bound for N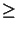 1 is given by (cf. (D.2))
1 is given by (cf. (D.2))
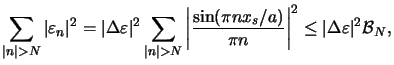 |
(D.8) |
with
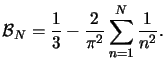 |
(D.9) |
The bound is obtained by replacing
| sin(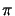 nxs/a)| with unity, i.e.,
nxs/a)| with unity, i.e.,
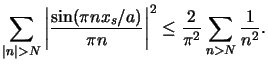 |
(D.10) |
The right-hand side equals
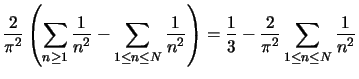 |
(D.11) |
since
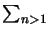 n-2 =
n-2 = 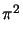 /6.
Inserting (D.7)
and (D.8) into (D.6) yields
/6.
Inserting (D.7)
and (D.8) into (D.6) yields
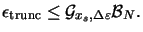 |
(D.12) |
with
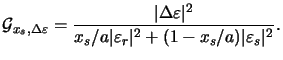 |
(D.13) |
(D.12) shows that the bound consists of a geometrical factor
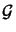 xs,
xs,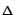
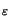 and a numerical factor
and a numerical factor
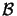 N.
The geometrical factor
N.
The geometrical factor
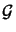 xs,
xs,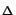
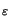 (cf. (D.13))
is proportional to the squared difference
|
(cf. (D.13))
is proportional to the squared difference
|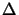
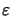 |2 = |
|2 = |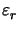 -
- 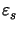 |2
of the resist and step material permittivities.
The truncation error
|2
of the resist and step material permittivities.
The truncation error
 is thus governed by the strength of the inhomogeneity, which is in
accordance with physical considerations. The dependence of the numerical factor
is thus governed by the strength of the inhomogeneity, which is in
accordance with physical considerations. The dependence of the numerical factor
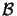 N (cf. (D.9)) on the truncation
frequency N is plotted for a constant
N (cf. (D.9)) on the truncation
frequency N is plotted for a constant
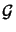 xs,
xs,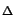
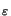 in Figure D.2. In this figure
also an exact expression for the special situation xs = a/2 is shown, i.e.,
the case when the intersection point xs lies in the middle of the interval
[0, a]. In this case the truncation error
in Figure D.2. In this figure
also an exact expression for the special situation xs = a/2 is shown, i.e.,
the case when the intersection point xs lies in the middle of the interval
[0, a]. In this case the truncation error
 of (D.6) can be exactly calculated like
whereby
of (D.6) can be exactly calculated like
whereby
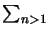 (2n - 1)-2 =
(2n - 1)-2 = 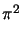 /8 is used.
Both expressions (D.12) and (D.14) show that for
increasing N the error decreases quadratically.
/8 is used.
Both expressions (D.12) and (D.14) show that for
increasing N the error decreases quadratically.
Figure D.2:
Truncation error
 of the second derivative
(cf. (D.6)) as a function of the cut-off frequency N.
The geometrical factor is set equal to unity. Both the
bound (D.12) and the exact expression (D.14)
obtained for xs = a/2 are shown in linear and logarithmic
scale, upper and lower graph, respectively. For increasing
N the error decreases quadratically.
of the second derivative
(cf. (D.6)) as a function of the cut-off frequency N.
The geometrical factor is set equal to unity. Both the
bound (D.12) and the exact expression (D.14)
obtained for xs = a/2 are shown in linear and logarithmic
scale, upper and lower graph, respectively. For increasing
N the error decreases quadratically.
|
|
As a final remark note that (D.6) describes the error of the
second derivative at one
single vertical point zc. The overall discretization error depends
on the number Nz of vertical grid points.
Footnotes
- ... function.a
- Heaviside's step
function is defined as
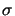 (x) = 0 for x < 0 and 1 otherwise.
(x) = 0 for x < 0 and 1 otherwise.
- ...
satisfyb
- For TE-polarization the three field components Ex(z),
Ez(z), and
Hy, nm(z) vanish [11, p. 52]. Taking the
remaining three field components Ey(z), Hx(z), and Hz(z)
in (6.15) and (6.18) and eliminating the
latter two yields (D.3).




Next: Bibliography
Up: PhD Thesis Heinrich Kirchauer
Previous: C.2 Stack of Homogeneous
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17


![]() (x) of the permittivity is simply given by
(cf. Figure D.1)
(x) of the permittivity is simply given by
(cf. Figure D.1)
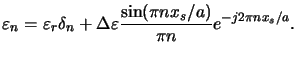
![$\displaystyle \frac{d^2 E_{y,n}(z)}{dz^2} = \sum_{m}\left[k_{x,n}^2\delta_{nm}-k_0^2\varepsilon_{n-m}(z)\right]E_{y,m}(z).$](img1654.gif)
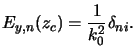
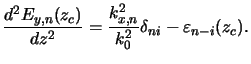
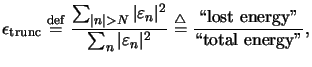
![]() .
For that we first evaluate the denominator occurring
in (D.6) with the
help of Parseval's theorem [131, p. 224] to (cf. (D.1))
.
For that we first evaluate the denominator occurring
in (D.6) with the
help of Parseval's theorem [131, p. 224] to (cf. (D.1))
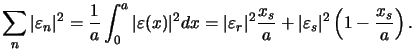
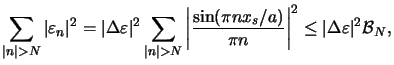
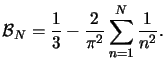
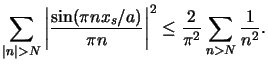
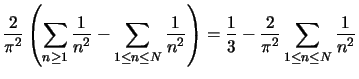
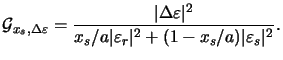
![$\displaystyle \begin{aligned}\epsilon_{\mathrm{trunc}} &= \mathcal{G}_{x_s,\Del...
...2}{\pi^2}\sum_{n=1}^{\lfloor N/2\rfloor} \frac{1}{(2n-1)^2}\bigg],\end{aligned}$](img1691.gif)