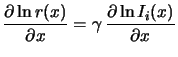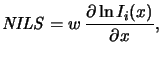Next: 3.2.3 Lumped Parameter Model
Up: 3.2 Practical Characterization
Previous: 3.2.1 Focus Effects and
Full optimization of a lithography process requires thorough and
time-consuming calculations of many effects. One simplified approach to this
optimization problem is to perform limited calculations at one point in
space, e.g., the nominal line edge. The optimization of certain important
lithographic parameters is then performed only at this point.
In spite of its restriction on a single point the method has often physical
significance and the results can be very useful. Additional simplifications of
the analysis are achieved by separating the effects of the lithography
tool from that of the resist process. This can be done with
reasonable accuracy only if the interaction of the imaging tool with the
photoresist is known.
The lithographic imaging equation [49,50]
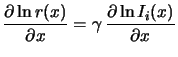 |
(3.1) |
relates the aerial image intensity Ii(x) to the development
rate r(x) of the photoresist, whereby the lumped parameter 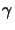 denotes
the resist contrast and x is the horizontal position in the mask/wafer plane
relative to the investigated point. The gradient of the logarithm of the aerial
image is simply called the log-slope. As can be seen
from (3.1) the development rate gradient in
lateral direction and thus the resolution is either maximized by higher resist
contrast or by a larger log-slope of the aerial image.
denotes
the resist contrast and x is the horizontal position in the mask/wafer plane
relative to the investigated point. The gradient of the logarithm of the aerial
image is simply called the log-slope. As can be seen
from (3.1) the development rate gradient in
lateral direction and thus the resolution is either maximized by higher resist
contrast or by a larger log-slope of the aerial image.
Equation (3.1) clearly indicates that the aerial image log-slope
is a proper metric to judge the performance of the imaging tool.
In particular, the image log-slope, when normalized by multiplication
with the feature width w, is directly proportional to exposure latitude
expressed as a percent change in exposure to give a percent change in linewidth.
The normalized image log-slope
NILS [49,50], thus defined
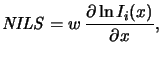 |
(3.2) |
has proven to be a powerful metric for optimizing lithography processes
by means of simulation [51,52]. The resolution of
different features can be conveniently studied by plotting the
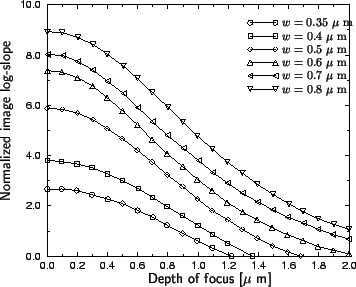
normalized image log-slope versus defocus. As shown in
Figure 3.4 the depth of focus is extremely sensitive to the
feature size, a fact that is not evident in the theoretical Rayleigh definition
given by (2.2). Hence, resolution and depth of focus cannot be
defined independently, but are rather interdependent.
Figure 3.4:
The normalized image
log-slope is directly proportional to exposure latitude and has
proven to be a powerful metric in lithography optimization.
|
|
Although defocus is a strictly optical phenomenon, the photoresist plays a
significant role in determining focus effects. Principally, a better photoresist
provides a greater depth of focus,
i.e., the minimum acceptable log-slope specification
is lower resulting in a larger usable focus range. This relationship between
photoresist and the log-slope specification can be determined experimentally
by measuring focus-exposure matrices like in Figure 3.2
for many different feature types and sizes. The resulting correlation
between normalized image log-slope
NILS and
exposure latitude
EL is typically expressed by
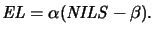 |
(3.3) |
Here 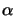 is the percent in increase of exposure latitude
EL per
unit increase of
NILS, and
is the percent in increase of exposure latitude
EL per
unit increase of
NILS, and 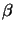 is the minimum
NILS
required to give any image at all in the photoresist. Thus, to a first degree
the effect of the photoresist on depth of focus can be characterized by
the two parameters
is the minimum
NILS
required to give any image at all in the photoresist. Thus, to a first degree
the effect of the photoresist on depth of focus can be characterized by
the two parameters 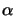 and
and 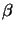 . For an ideal, infinite contrast resist
it can be shown that
. For an ideal, infinite contrast resist
it can be shown that 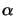 = 10 and
= 10 and 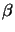 = 0 [53]. The quality of a
photoresist with respect to focus and exposure latitude can now be judged by how
close
= 0 [53]. The quality of a
photoresist with respect to focus and exposure latitude can now be judged by how
close 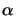 and
and 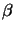 are to these ideal values.
are to these ideal values.




Next: 3.2.3 Lumped Parameter Model
Up: 3.2 Practical Characterization
Previous: 3.2.1 Focus Effects and
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17