



Next: 4.1.1 Scalar Diffraction Theory
Up: 4. Aerial Image Simulation
Previous: 4. Aerial Image Simulation
4.1 Principles of Fourier Optics
The foundations of scalar diffraction theory can directly be derived
from the most rigorous physical description of light, namely from
the Maxwell equations. Applying certain approximations to the general results
yields closed-form expressions valid in the optical far field.
These approximations combined with a simple model for
the phase transformation property of a thin lens establish the
Fourier analysis of an imaging system.
If the problem is further restricted to Köhler
illumination [11, pp. 524-526]
and periodic mask patterns, Fast Fourier Transform (FFT) algorithms can be
useful for an efficient evaluation of the resulting formulae.
Usually the scalar version of Fourier optics is based on the
paraxial approximation [111, p. 80], i.e., the angles of the light rays
to the optical axis are assumed to be sufficiently small so that small angle
approximations can be made. This assumption holds up to numerical
apertures of
NA 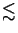 0.5 [66]. By not imposing the
paraxial approximation scalar models can be applied to
NA
0.5 [66]. By not imposing the
paraxial approximation scalar models can be applied to
NA 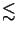 0.6 [112]. For higher numerical aperture
systems polarization effects cannot be neglected and vector diffraction
theory is clearly needed to account for the polarization and the inherent
coupling between the vector components of the electromagnetic
field [113]. For
NA
0.6 [112]. For higher numerical aperture
systems polarization effects cannot be neglected and vector diffraction
theory is clearly needed to account for the polarization and the inherent
coupling between the vector components of the electromagnetic
field [113]. For
NA 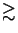 0.6 the vector-valued
pendant [114] to the scalar theory of Fourier optics has to be used.
0.6 the vector-valued
pendant [114] to the scalar theory of Fourier optics has to be used.




Next: 4.1.1 Scalar Diffraction Theory
Up: 4. Aerial Image Simulation
Previous: 4. Aerial Image Simulation
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17