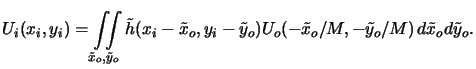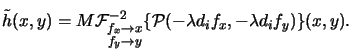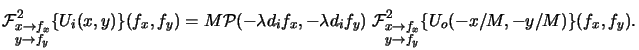Next: 4.1.4 Köhler Illumination of
Up: 4.1 Principles of Fourier
Previous: 4.1.2 Phase Transformation Properties
In the preceding two sections diffraction phenomena in the optical far field
and the imaging properties of a single thin converging lens were
studied. The resulting formulae (4.11) and
(4.19) establish linear relations between the
optical field at different spatial coordinates.
In view of this linearity of the wave propagation phenomenon, a general
linear superposition integral is postulated to describe imaging
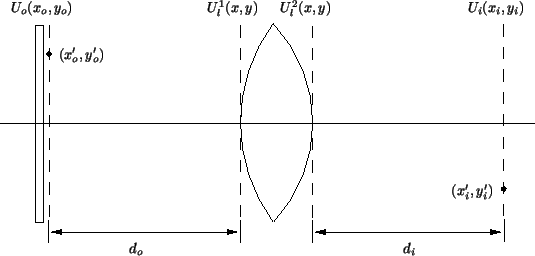
formation with a lens configuration similar to that shown in
Figure 4.4. The image amplitude
Ui(xi, yi) is related to
the object amplitude
Uo(xo, yo) by
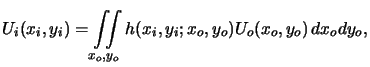 |
(4.21) |
whereby (xi, yi) and (xo, yo) are the image and object coordinates,
respectively. Theoretically, the kernel
h(xi, yi;xo, yo) equals the image
amplitude
Ui(xi, yi), if the object is an ideal unit-amplitude point source
located at
(xo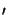 , yo
, yo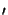 ), i.e.,
), i.e.,
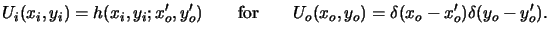 |
(4.22) |
Figure 4.4:
Image formation with a lens. The image
amplitude
Ui(xi, yi) is related to the object amplitude
Uo(xo, yo) by
a linear superposition integral.
|
|
How can we determine the kernel
h(xi, yi;xo, yo) in practice?g
First, we recall that a spherical wave diverging from the point source
travels towards the lens. The amplitude incident on the lens
is given by
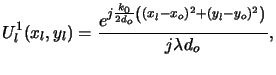 |
(4.23) |
whereby we have readily employed the paraxial approximation.
After passage through the lens, the field distribution writes with
(4.19) and (4.21) as
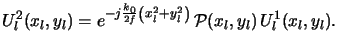 |
(4.24) |
Finally, the image amplitude is given by the Fresnel approximation of
(4.14),
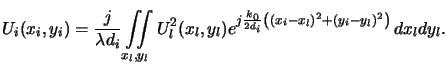 |
(4.25) |
The impulse response looked for follows now from the above three equations to
![$\displaystyle h(x_i,y_i;x_o,y_o) \cong \frac{1}{\lambda^2 d_o d_i} \iint\limits...
...ight)x_l + \left(\frac{y_o}{d_o}+\frac{y_i}{d_i}\right)y_l \right]} \,dx_ldy_l,$](img405.gif) |
(4.26) |
whereby we have neglected the two quadratic phase factors
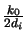 (xi2 + yi2) and
(xi2 + yi2) and
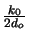 (xo2 + yo2).
The first factor
(xo2 + yo2).
The first factor
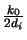 (xi2 + yi2) can be eliminated
by noting that we are primarily interested in the intensity distribution of
the image, i.e., in the square module of the image amplitude. The second
phase factor
(xi2 + yi2) can be eliminated
by noting that we are primarily interested in the intensity distribution of
the image, i.e., in the square module of the image amplitude. The second
phase factor
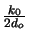 (xo2 + yo2) cannot simply be dropped as it
depends on the integration variables (xo, yo) of (4.24).
However, assuming that the
image amplitude at (xi, yi) consists only of object contributions
from a tiny region located around
(xo, yo) = - M(xi, yi),
we approximately get
exp(
(xo2 + yo2) cannot simply be dropped as it
depends on the integration variables (xo, yo) of (4.24).
However, assuming that the
image amplitude at (xi, yi) consists only of object contributions
from a tiny region located around
(xo, yo) = - M(xi, yi),
we approximately get
exp(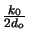 (xo2 + yo2))
(xo2 + yo2)) 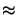 exp(
exp(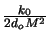 (xi2 + yi2)).
The quantity M is the magnification of the system and will be defined soon
(cf. (4.31)).
Because the dependence on the object space coordinates has been removed,
the second phase factor can be dropped following the same arguments as for
the first one.
(xi2 + yi2)).
The quantity M is the magnification of the system and will be defined soon
(cf. (4.31)).
Because the dependence on the object space coordinates has been removed,
the second phase factor can be dropped following the same arguments as for
the first one.
As a final simplification, we restrict our attention to a particular plane
behind the lens, namely that for which the image plane distance di satisfies
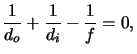 |
(4.27) |
and
1/f > 1/d0 so that
1/di = 1/f - 1/d0 > 0 holds.
This relation is well-known in geometrical optics and is usually called
the lens law.
To achieve a compact and physically predicative form for the
kernel (4.29)
we now introduce the magnification of the projection system as
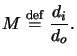 |
(4.28) |
Using the magnification thus defined to scale the object coordinates and
introducing spatial frequencies for the lens coordinates,
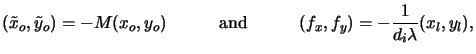 |
(4.29) |
a scaled version
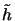 (xi, yi;
(xi, yi;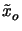 ,
,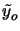 ) of the
kernel (4.29)h
) of the
kernel (4.29)h
![$\displaystyle \tilde{h}(x_i,y_i;\tilde{x}_o,\tilde{y}_o) \cong M\iint\limits_{f...
..._y) e^{j2\pi\left[(x_i-\tilde{x}_o)f_x+(y_i-\tilde{y}_o)f_y\right]} \,df_xdf_y.$](img424.gif) |
(4.30) |
This relation is of fundamental importance for the Fourier analysis of an
imaging system as it not only determines the kernel of the superposition integral
(4.24), but also shows the shift-invariance of it, i.e.,
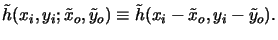 |
(4.31) |
This means that the relation between object and image field is
a convolution integral,
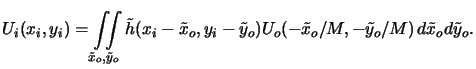 |
(4.32) |
As can be seen from (4.33) the kernel or the impulse response
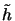 (x, y) is the inverse Fourier transformi
of a scaled version of the pupil function
(x, y) is the inverse Fourier transformi
of a scaled version of the pupil function
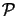 (x, y), i.e.,
(x, y), i.e.,
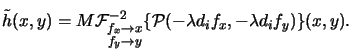 |
(4.33) |
With the convolution theoremj
of the Fourier transform we can transform (4.35)
into the frequency domain and obtain the following simple relation between
object and image spectrum:
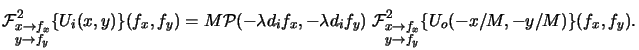 |
(4.34) |
This equation is in accordance with geometrical optics, since as 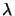 approaches zero the range over which
approaches zero the range over which
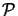 (-
(- 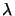 difx, -
difx, - 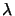 dify) equals unity will grow without
bounds allowing it to be replaced by unity. Hence, in the limiting
case
dify) equals unity will grow without
bounds allowing it to be replaced by unity. Hence, in the limiting
case
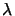
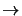 0 the object and image are
related by
Ui(x, y) = MUo(- x/M, - y/M), i.e., the image is an exact replica
of the object, magnified and inverted in the image plane.
0 the object and image are
related by
Ui(x, y) = MUo(- x/M, - y/M), i.e., the image is an exact replica
of the object, magnified and inverted in the image plane.
Footnotes
- ... practice?g
- In
the subsequent derivation (xo, yo) refers to the point source location in
the object space instead of
(x
 o, y
o, y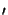 o).
The difference between the fixed location
(x
o).
The difference between the fixed location
(x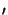 o, y
o, y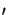 o) and the
coordinates (xo, yo) is clear throughout the discussion anyway.
o) and the
coordinates (xo, yo) is clear throughout the discussion anyway.
- ...)h
- The scaled kernel is defined by
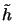 (xi, yi;
(xi, yi;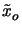 ,
,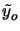 ) = h(xi, yi; -
) = h(xi, yi; - 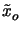 /M, -
/M, - 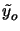 /M).
/M).
- ... i
- The Fourier
transform F(y) of a function f (x) is defined as
F(y) =
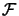 x
x 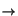 y{f (x)}(y)
y{f (x)}(y)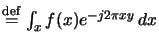 and its inverse is given by
f (x) =
and its inverse is given by
f (x) = 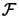 -1y
-1y 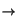 x{F(y)}(x)
x{F(y)}(x)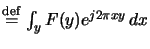 .
.
- ... j
- The convolution theorem states that
the Fourier transform of a convolution integral
(h*f )(x) =
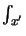 h(x - x
h(x - x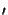 )f (x
)f (x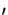 ) dx
) dx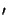 of two
functions h(x) and f (x) equals the product of the two Fourier
transforms H(y) and F(y), i.e.,
of two
functions h(x) and f (x) equals the product of the two Fourier
transforms H(y) and F(y), i.e.,
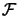 x
x  y{(h*f )(x)}(y) = H(y) F(y).
y{(h*f )(x)}(y) = H(y) F(y).




Next: 4.1.4 Köhler Illumination of
Up: 4.1 Principles of Fourier
Previous: 4.1.2 Phase Transformation Properties
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
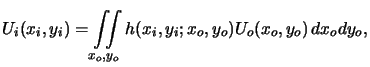
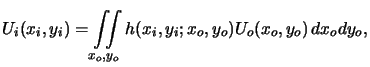
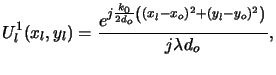
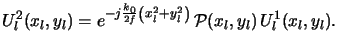
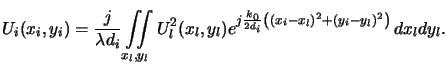
![$\displaystyle h(x_i,y_i;x_o,y_o) \cong \frac{1}{\lambda^2 d_o d_i} \iint\limits...
...ight)x_l + \left(\frac{y_o}{d_o}+\frac{y_i}{d_i}\right)y_l \right]} \,dx_ldy_l,$](img405.gif)
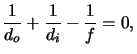
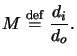
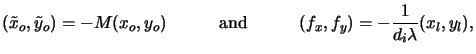
![$\displaystyle \tilde{h}(x_i,y_i;\tilde{x}_o,\tilde{y}_o) \cong M\iint\limits_{f...
..._y) e^{j2\pi\left[(x_i-\tilde{x}_o)f_x+(y_i-\tilde{y}_o)f_y\right]} \,df_xdf_y.$](img424.gif)