Next: 4.1.5 Vector-Valued Extension
Up: 4.1 Principles of Fourier
Previous: 4.1.3 Fourier Analysis of
The most important configuration of the illuminator in projection printing
systems is due to Köhler [11, pp. 524-526].
In this method a converging lens commonly
called condenser is positioned in front of the light source, whereby
the light source lies in the focal plane of the lens
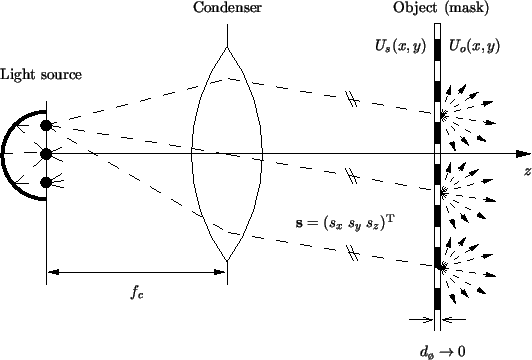
(cf. Section 2.3.2). As illustrated in
Figure 4.5 the rays from each source point then emerge
from the condenser as parallel beams. This arrangement has the advantage
that irregularities in the brightness distribution on the source do not
cause irregularities in the intensity of the object illumination. Thus
the quality of image composition severely depends on a careful and accurate
set-up of the Köhler arrangement. For the mathematical description we
assume an ideal set-up, so that the emerging beams from one source point
form--after passage through the condenser--a plane wave.
In complex phasor notation we get for the disturbance on the object
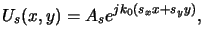 |
(4.35) |
with amplitude As and normalized wavevector
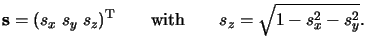 |
(4.36) |
Figure 4.5:
Köhler illumination of an
object. The Köhler arrangement provides a plane wave illumination
of the mask. The quality of the image composition severely depends on
an accurate set-up.
|
|
In photolithography the object to be imaged is the photomask, whereby the
pattern is either exclusively stored in the amplitude transmittance or in
both amplitude and phase. Technological aspects of binary and
phase-shifting masks were already discussed in Section 2.4.
For aerial image simulation the mask is modeled to be infinitesimally thin
with ideal transitions of the transmission characteristic, i.e., the mask
thickness
dø vanishes as shown in
Figure 4.5. Depending
on the mask type, the so-called transmission function t(x, y) is real-valued
(zero or one) or complex-valued with module less than one. Similar
to the phase transformation of the lens in (4.19)
the field disturbance Us(x, y) incident on the mask is multiplied with
the transmission function t(x, y) to obtain the object field immediately
behind the mask, i.e.,
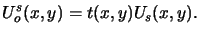 |
(4.37) |
This relation holds for the same reasons as discussed in connection with
the Kirchhoff boundary conditions below (4.6) on
page ![[*]](cross_ref_motif.gif) .
For Köhler illumination we get with (4.38)
for the object amplitude
.
For Köhler illumination we get with (4.38)
for the object amplitude
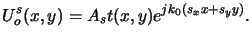 |
(4.38) |
Now we make a fundamental assumption that is used throughout all aerial
image simulators: The photomask is periodic in both lateral
directions x and y with periods a/M and b/M, respectively, i.e.,
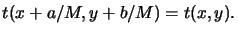 |
(4.39) |
The object periods are chosen as a/M and b/M, so that the image periods
are a and b for a M : 1-projection system (cf. (4.37)).
A direct consequence of this assumption is the possibility to represent
the transmission function t(x, y) by a Fourier series, i.e.,
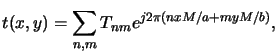 |
(4.40) |
whereby the Fourier coefficients are given by
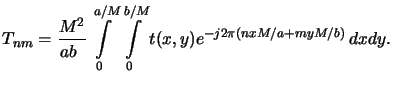 |
(4.41) |
Combining the two equations (4.41)
and (4.43) yields for the object amplitude
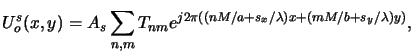 |
(4.42) |
whereby
k0 = 2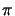 /
/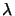 has been inserted for the wavenumber. The object
coordinates have to be scaled by the magnification M resulting in
(cf. (4.35))
has been inserted for the wavenumber. The object
coordinates have to be scaled by the magnification M resulting in
(cf. (4.35))
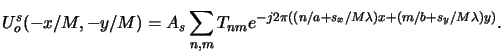 |
(4.43) |
Next we restrict the source point locations to a rectangular grid.
Hence, only homogeneous plane waves from certain discrete orientations
have to be considered further. We choose the spacing of the grid in the
source plane in such a way that the lateral components of
the normalized wavevector
spq equal
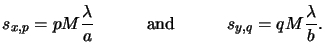 |
(4.44) |
The reason for this discretization will be explained later.
Throughout aerial image simulation, it is more or less
irrelevant although the resulting formulae are more compact. However,
for an efficient exposure/bleaching simulation this specific choice
is crucial as will be explained in Chapter 6.
Insertion of the discrete wavevectors (4.47)
into (4.46) yields
for the scaled object amplitude due to one source point (p, q).
Because of the periodicity of
Uopq(- x/M, - y/M) its Fourier transform
consists of a train of impulses occurring at the harmonically related
frequencies n/a and m/b and writes to
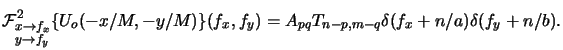 |
(4.45) |
Now we can easily determine the image spectrum from (4.37).
Employing the equivalence property of the delta-functionk
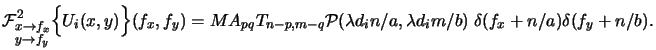 |
(4.46) |
Consequently, we obtain a Fourier series representation for the image such as
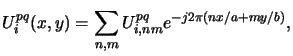 |
(4.47) |
whereby the Fourier coefficients are given by
As can be seen the discrete pupil function P(n, m) is related to the real
physical pupil function
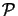 (x, y) by
P(n, m) = M
(x, y) by
P(n, m) = M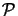 (
(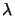 din/a,
din/a,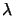 dim/b) and writes
with (4.22) to
dim/b) and writes
with (4.22) to
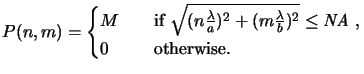 |
(4.49) |
The intensity
Iipq(x, y) due to the illumination of the mask
by one source point (p, q) is simply the squared module of the amplitude
divided by two-times the free-space resistance  ,l
i.e.,
,l
i.e.,
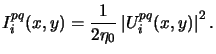 |
(4.50) |
Footnotes
- ... delta-functionk
- The equivalence
or filtering property of the delta function
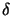 (x) states that
f (x) = h(x)
(x) states that
f (x) = h(x)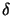 (x - x
(x - x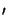 ) equals
f (x) = h(x
) equals
f (x) = h(x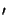 )
)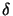 (x - x
(x - x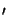 ).
).
- ...
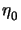 ,l
,l
- The free-space
resistance has a value of
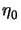 =
= 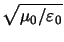
 377
377 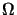 .
.




Next: 4.1.5 Vector-Valued Extension
Up: 4.1 Principles of Fourier
Previous: 4.1.3 Fourier Analysis of
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
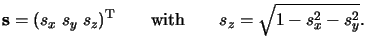
![[*]](cross_ref_motif.gif) .
For Köhler illumination we get with (4.38)
for the object amplitude
.
For Köhler illumination we get with (4.38)
for the object amplitude
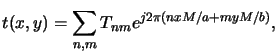
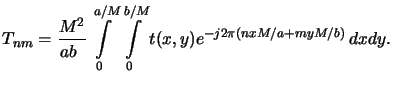
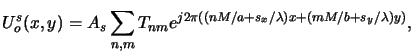
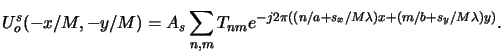
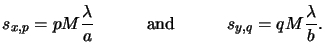
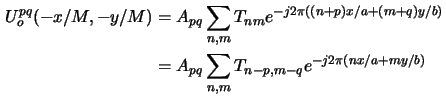
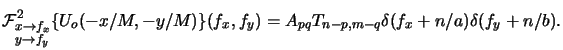
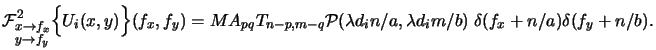
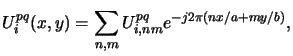
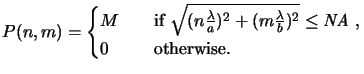
![]() ,l
i.e.,
,l
i.e.,