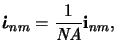
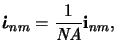 |
(4.63) |
| (4.64) |
The power series expansion of the aberration function takes the form [117,118]
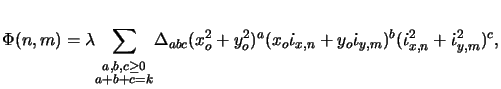 |
(4.65) |
|
Although the expansion of (4.74) is a general representation
of the aberration function in that any aberration function ![]() (n, m)
can be represented,
other polynomials are more suited to describe higher-order aberration terms.
(n, m)
can be represented,
other polynomials are more suited to describe higher-order aberration terms.