![$\displaystyle \Phi(n,m)= \lambda\!\sum_{\begin{Sb}a,b\ge0,\;c\\ [1mm]a-\vert c\...
...mathrm{even}\end{Sb}} \!\Delta_{abc}A_{ac}\mathcal{Z}_b^c(\rho_{nm},\phi_{nm}).$](img610.gif)
![$\displaystyle \Phi(n,m)= \lambda\!\sum_{\begin{Sb}a,b\ge0,\;c\\ [1mm]a-\vert c\...
...mathrm{even}\end{Sb}} \!\Delta_{abc}A_{ac}\mathcal{Z}_b^c(\rho_{nm},\phi_{nm}).$](img610.gif) |
(4.66) |
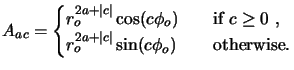 |
(4.67) |
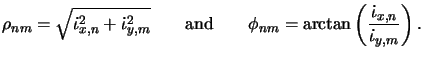 |
(4.68) |
The Zernike polynomials in real-valued form are defined as
![$\displaystyle \mathcal{Z}_b^c(\rho,\phi) \overset{\mathrm{def}}{=}\begin{cases}...
... [2mm] \mathcal{R}_b^c(\rho) \sin(c\phi) & \quad{} \text{otherwise,}\end{cases}$](img618.gif) |
(4.69) |
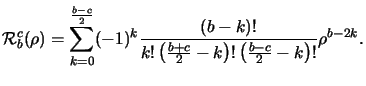 |
(4.70) |
|
The lens aberrations have a variety of impacts on the lithographic performance [117,119]. The most severe problems are shifts in the image position, image asymmetry, reduction of the process window, and the appearance of undesirable imaging artifacts. Aerial image simulation provides a powerful tool to investigate most of them. In Table 4.3 the imaging consequences of the first 11 Zernike polynomials are listed.
|