4.2.4 In-Lens Filters

Spatial filtering at the lens pupil enhances the depth of focus while maintaining high resolution capability in optical lithography. From a physical point of view, in-lens filtering can be interpreted as an amplitude superposition of plural images at different focal planes with a controlled phase difference between them [21]. The technique of multiple exposures at different focus levels was first introduced by Hiroshi Fukuda et al. and is called FLEX [121,122]. It is closely related to the phase-shifting approach (cf. Section 2.4.2), which realizes the phase-controlled amplitude superposition in lateral direction instead of in axial direction as with FLEX.

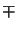
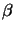
The operation principle can easily be demonstrated as follows: From (4.51), (4.52) and (4.69), (4.70) we obtain for the coherent superposition of two focus levels z = $\mp$ $\beta$

$$\begin{aligned}U_i^{pq}(x,y) &= \frac{1}{2}\sum_{n,m} A_{pq} T_{n... ... e^{-j\delta}e^{-jk_0\beta i_{z,nm}}\right] e^{-j2\pi(nx/a+mq/b)},\end{aligned}$$

whereby the two contributions have the same amplitude A_pq/2 but a phase difference of 2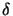$\delta$. Hence the composite spectrum equals

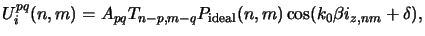$$U_i^{pq}(n,m) = A_{pq} T_{n-p,m-q} P_{\mathrm{ideal}}(n,m)\cos(k_0\beta i_{z,nm} + \delta),$$ (4.71)

and the filter function F(n, m) is extracted to (cf. (4.69))

 

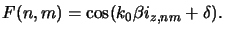$$F(n,m) = \cos(k_0\beta i_{z,nm} + \delta).$$ (4.72)

Alternatively, the cosine term (4.82) can be added to the Fourier coefficients T_nm of the mask [123], which is the principle of the phase-shifting approach [16]. As can be seen from (4.82) the shape of the filter function F(n, m) depends on the distance 2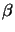$\beta$ as well as the phase difference 2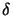$\delta$ between the two planes. Both parameters can easily be controlled and thus the filter function can be optimized. For single features, e.g., a hole pattern, a depth of focus three times larger with a 20% improved resolution limit can be achieved, whereas for a general VLSI pattern the depth of focus enhancement is smaller but still ranges from 1.5-1.7 [21]. However, this improvement comes at the expense of decreasing radial energy concentration in the point spread function and decreasing overall energy flux through the pupil [22]. The first limitation appears to be more serious, since decreasing pupil transmission can, at least in principle, be compensated for by increasing the source intensity. On the other hand, the loss of energy in the central maximum in comparison to the secondary maxima results in a loss of contrast in the image.

From a practical point of view, it is rather difficult to obtain a continuous transmission distribution of a filter as given in (4.82). Thus a simplified filter structure has to be applied, which reduces the performance gain only slightly. Additionally, the control of lens aberrations becomes very difficult since the method modifies the core part of the lens. Finally, light reflection and absorption in the filter are serious practical engineering problems because the image quality is degraded by flare and the absorption causes heat load problems.