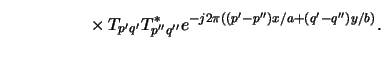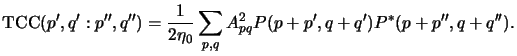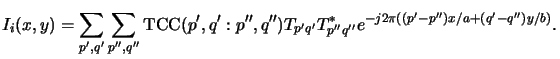Next: 4.4 Numerical Implementation
Up: 4.3 Advanced Illumination Aperture
Previous: 4.3.1 Abbe's Method
4.3.2 Hopkins' Method
As already mentioned Hopkins' method is based on the exchange of the
integration order over the point source contributions and the diffraction
amplitudes, which has the advantage that a given optical system with fixed
illumination, numerical aperture, defocus, and other aberrations can be
described with the so-called transmission cross coefficients (TCCs).
The TCCs need to be calculated just once. Thereafter
they can be reused for repeated aerial image simulations of
different mask patterns printed by the same optical system.
We will now derive the Hopkins' formulae only for the scalar aerial image
calculation. The resulting relations are the discretized equivalents to
those presented in [117]. The extension to the vector case is
obvious and can be found in the literature, e.g., in [127].
The aerial image Ii(x, y) is the incoherent superposition of the individual
point source contributions
Iipq(x, y) (cf. (4.83)).
In the scalar theory these contributions are given by (4.54).
With (4.51) and (4.52) the aerial
image is explicitly written as
Next we perform a change of summation indices like:
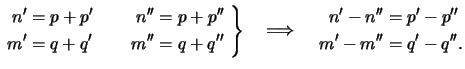 |
(4.87) |
By exchanging the summation order in (4.96)
the aerial image is obtained as
The term in square brackets defines the TCCs, i.e.,
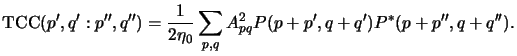 |
(4.89) |
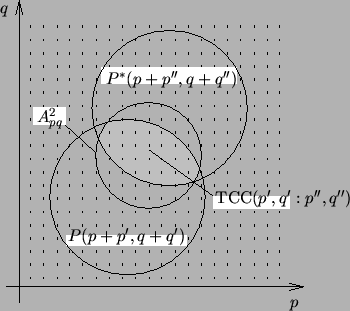
The range of the various summation indices is
illustrated in Figure 4.9
for the case of a circular-shaped illumination cone and pupil function.
Hence, once the TCCs are calculated from (4.99) the aerial
image can easily be determined for a fixed optical system from
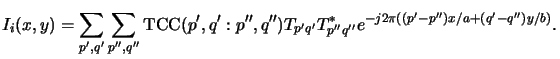 |
(4.90) |
Figure 4.9:
Transmission cross coefficients (TCCs) of
Hopkins' method of partially coherent illumination with circular
aperture and lens. The shaded area illustrates the range of the
summation indices (p, q) in (4.99)
(after [11, p. 531]).
|
|




Next: 4.4 Numerical Implementation
Up: 4.3 Advanced Illumination Aperture
Previous: 4.3.1 Abbe's Method
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
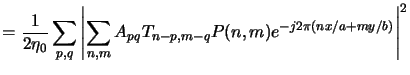
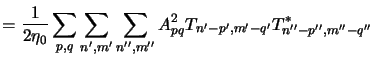
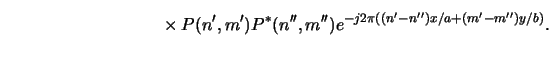
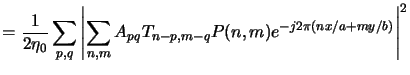
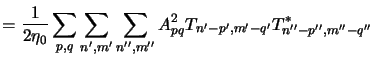
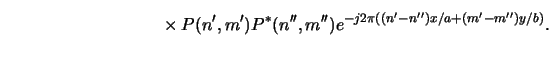
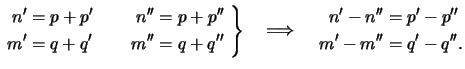
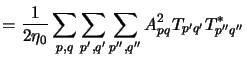
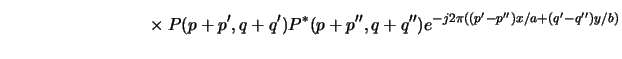
![$\displaystyle = \sum_{p^\prime,q^\prime}\sum_{p^{\prime\prime},q^{\prime\prime}...
...{pq} P(p+p^\prime,q+q^\prime)P^*(p+p^{\prime\prime},q+q^{\prime\prime}) \right]$](img712.gif)