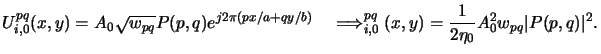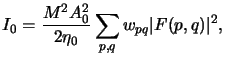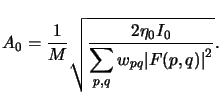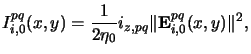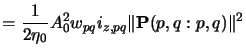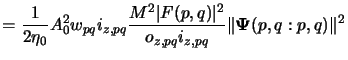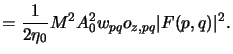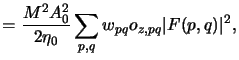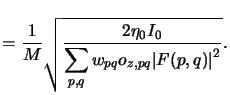Next: 4.3.2 Hopkins' Method
Up: 4.3 Advanced Illumination Aperture
Previous: 4.3 Advanced Illumination Aperture
4.3.1 Abbe's Method
Following Abbe the image due to one coherent source point is first calculated.
Either the scalar formulation of (4.54) or
the vector form of (4.68) can be used.
The aerial image is then obtained by an incoherent superposition of all the
contributions and formally writes to
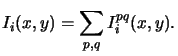 |
(4.73) |
The point sources (p, q) are located within the illumination
aperture. Beside this no further restrictions on the shape of the aperture
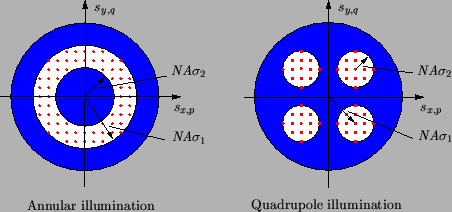
are made. Examples for annular and quadrupole illumination are shown in
Figure 4.7.
Figure 4.7:
Source discretization of an annular and quadrupole
illumination system. To account for arbitrary illumination forms
the light source is discretized into mutually independent coherent
point sources located inside the illumination aperture.
|
|
The spacing between the individual point sources has to satisfy a
specific criterion. As mentioned before, it is chosen in such a way that
the lateral wavevector components sx, p and sy, q
of the waves incident on the photomask equal an integer
multiple of the sampling frequencies
M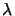 /a and
M
/a and
M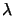 /b
(cf. (4.47)). This choice guarantees that the
image on the wafer surface is periodic with periods a and b, which
becomes extremely important in context with the
exposure/bleaching simulation described in Chapter 6.
This requirement
is illustrated in the wavevector diagram of Figure 4.8 for the
case of conventional illumination.
/b
(cf. (4.47)). This choice guarantees that the
image on the wafer surface is periodic with periods a and b, which
becomes extremely important in context with the
exposure/bleaching simulation described in Chapter 6.
This requirement
is illustrated in the wavevector diagram of Figure 4.8 for the
case of conventional illumination.
Figure 4.8:
Source discretization of a conventional partially coherent
illumination system. The spacing between the individual point sources
is chosen to yield a periodic field incident on the photomask.
|
|
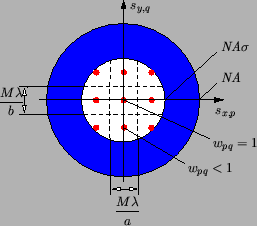
What is missing now is the determination of the amplitudes Apq
of the point sources. Clearly, they depend on the total imaging
intensity I0 as well as on the discretization scheme illustrated in
Figure 4.8. The intensity of one point source is proportional
to the discretization area wpq. As it is also related
to the square of the light amplitude Apq2 we write
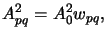 |
(4.74) |
where A0 is a simple normalizing constant.
By considering a missing or ``perfectly transparent'' mask,
we obtain the relationship between the amplitude Apq and
the total imaging intensity I0 looked for.
The transmission characteristic t(x, y) of a transparent mask equals to unity,
and its Fourier spectrum Tnm thus consists of a delta impulse at
zero frequency, i.e.,
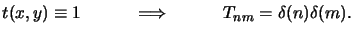 |
(4.75) |
The scalar and vector approach have to be studied separately from now on:
- Scalar theory.
With (4.84) and (4.85) the image
spectrum (4.52) writes as
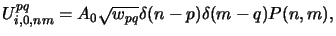 |
(4.76) |
and the image amplitude and intensity are obtained from
(4.51) and (4.54)
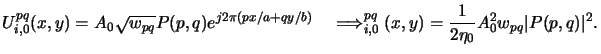 |
(4.77) |
The aerial image intensity
Ii, 0(x, y) is thus constant and with
the definition of the scalar pupil function (4.69)
found to be
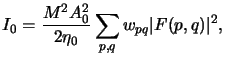 |
(4.78) |
whereby we assume that all point sources (p, q) are collected by the
projection lens, i.e., the numerical aperture of the condenser lens
must be smaller than that of the projection lens or, equivalently,
the partial coherence factor 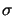 defined in (2.4) is smaller
than unity,
defined in (2.4) is smaller
than unity,
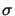
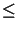 1.
From that the normalizing constant A0 can simply
be determined
1.
From that the normalizing constant A0 can simply
be determined
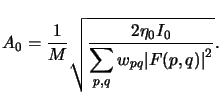 |
(4.79) |
- Vector theory.
The electric field amplitude (4.57) writes with
(4.84) and (4.85) to
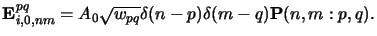 |
(4.80) |
Hence, in case of blank illumination a single homogeneous plane wave
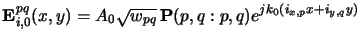 |
(4.81) |
is incident on the wafer.
For a homogeneous plane wave the vertical component of the Poynting
vector is simply given by
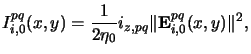 |
(4.82) |
and with (4.65) to (4.69)
the contribution of a single point source is calculated as follows:n
As expected the contributions
Ipqi, 0(x, y) are constant. Thus we obtain
for the blank aerial image
Footnotes
- ... follows:n
- For
(n, m) = (p, q) and thus
spq = opq we get from
(4.66) and (4.67)
|
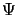 (p, q : p, q)|2 = oz, pq2.
(p, q : p, q)|2 = oz, pq2.




Next: 4.3.2 Hopkins' Method
Up: 4.3 Advanced Illumination Aperture
Previous: 4.3 Advanced Illumination Aperture
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
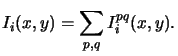
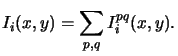
![]() /a and
M
/a and
M![]() /b
(cf. (4.47)). This choice guarantees that the
image on the wafer surface is periodic with periods a and b, which
becomes extremely important in context with the
exposure/bleaching simulation described in Chapter 6.
This requirement
is illustrated in the wavevector diagram of Figure 4.8 for the
case of conventional illumination.
/b
(cf. (4.47)). This choice guarantees that the
image on the wafer surface is periodic with periods a and b, which
becomes extremely important in context with the
exposure/bleaching simulation described in Chapter 6.
This requirement
is illustrated in the wavevector diagram of Figure 4.8 for the
case of conventional illumination.