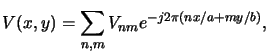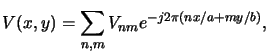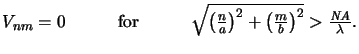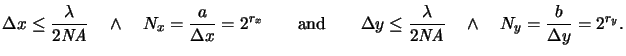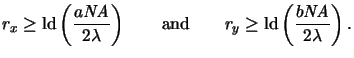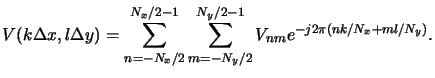Next: 5. Photoresist Exposure/Bleaching Simulation
Up: 4.4 Numerical Implementation
Previous: 4.4.1 ``Alias Free'' Forward
4.4.2 Numerical Backward Transform
In (4.51) and (4.55) we showed that
the source point contributions to the aerial image are obtained by Fourier
transforms like
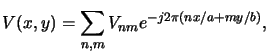 |
(4.97) |
whereby V(x, y) vicariously stands for the scalar or vector amplitude
Upqi(x, y) and
Epqi(x, y), respectively.
The spectrum Vnm of the source point contribution is
given either in (4.52) or (4.57)
depending on the chosen theory.
In both cases it is determined by the following three quantities:
source amplitude Apq, Fourier coefficients Tnm of the mask transfer
function, and discrete pupil function P(n, m) or
P(n, m : p, q).
For each of them formulae are provided in the preceding sections.
Hence, the spectrum can be calculated and the field is obtained by
evaluating the transform in (4.107). This last step
is accomplished as follows.
The finite extent of the pupil function in (4.53)
or (4.58) shows that the image spectrum is always a
low-pass function, i.e.,
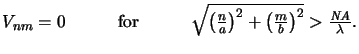 |
(4.98) |
Hence, the fundamental results of the
sampling theory [129,130] can be applied,
which state that any band-limited, finite-energy function f (x) can be
reconstructed from discrete equally-spaced samples
f (n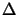 x), if the spacing
between the samples
x), if the spacing
between the samples 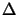 x meets the Nyquist criterion
x meets the Nyquist criterion
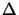 x
x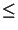 1/2W, whereby W is the highest frequency occurring in f (x).
Self-evidently the sampling theorem is also valid for functions defined in a
higher dimensional space. As can be seen from (4.108) the
aerial image spectrum Vnm is circularly band-limited with cut-off frequency
NA/
1/2W, whereby W is the highest frequency occurring in f (x).
Self-evidently the sampling theorem is also valid for functions defined in a
higher dimensional space. As can be seen from (4.108) the
aerial image spectrum Vnm is circularly band-limited with cut-off frequency
NA/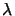 . Consequently, it suffices to evaluate the field V(x, y)
at discrete points only without any loss of information. We choose the spacings
. Consequently, it suffices to evaluate the field V(x, y)
at discrete points only without any loss of information. We choose the spacings
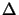 x and
x and 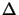 y to meet the Nyquist criterion and require that the
numbers of samples within the mask
periods Nx and Ny equal a power of two,q i.e.,
y to meet the Nyquist criterion and require that the
numbers of samples within the mask
periods Nx and Ny equal a power of two,q i.e.,
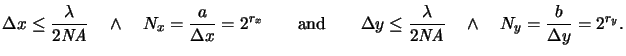 |
(4.99) |
Thus the powers
rx = ldNx and
ry = ldNy are chosen as the smallest
integers meeting
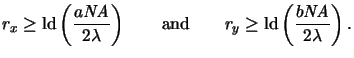 |
(4.100) |
The field disturbance on the equally spaced ortho-product grid is given now by
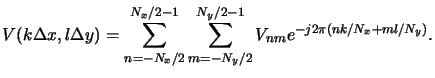 |
(4.101) |
This formula can efficiently be evaluated with a radix-2 FFT
algorithm [131, ch. 9], [132, ch. 12], [133, ch. 11].
We have chosen a public-domain software package that employs heavily inlined
FFT routines and precalculated weight tables to achieve maximal
speed.r
The length of the weight tables is 4096 and the unroll value is 128.
Above the unroll value conventional recursive routines are used.
To check the correctness of the algorithm we compared the results
with the well-established packet FFTPACK [134] from the
NETLIB.s
Information on the computational performance of the aerial image tool,
e.g., run-time and memory consumption, is given in connection with simulation
examples in Chapter 8.1.
Footnotes
- ... two,q
- The second requirement is
not obligatory, but the resulting formulae can then be evaluated with the most
efficient radix-2 FFT algorithm.
- ...
speed.r
- This package was written by Richard Krukar and is available
at http://hpux.u-aizu.ac.jp/hppd/hpux/Maths/Misc/ffts_in_C-1.0/readme.html.
- ...
NETLIB.s
- The package FFTPACK was written by Paul N. Swarztrauber
and is widely available, e.g., from the original NETLIB location
at http://www.netlib.org/fftpack/index.html.




Next: 5. Photoresist Exposure/Bleaching Simulation
Up: 4.4 Numerical Implementation
Previous: 4.4.1 ``Alias Free'' Forward
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17