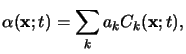Next: 5.1.2 Modeling of Conventional
Up: 5.1 Exposure Kinetics
Previous: 5.1 Exposure Kinetics
The basic law of light absorption in matter is an empirical one.
It postulates that the decrease of the light intensity
is proportional to the intensity itself. For a wave traveling in vertical
z-direction we thus write
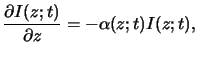 |
(5.1) |
whereby the generally spatial- as well as time-dependent quantity
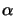 (z;t)
is the absorption coefficient of the medium. This
relation is commonly called Lambert's law [11, p. 614]
and has the interpretation of a
probability law, i.e., the probability that a photon will be absorbed
is proportional to the photon flux. Simple integration
(z;t)
is the absorption coefficient of the medium. This
relation is commonly called Lambert's law [11, p. 614]
and has the interpretation of a
probability law, i.e., the probability that a photon will be absorbed
is proportional to the photon flux. Simple integration
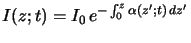 |
(5.2) |
yields the absorbance of the medium that is defined as the exponential
term in the above equation. The absorbance is the second important
characteristic quantity of the absorption phenomenon and often used as an
integral measure of the photoresist.
In case of a time-harmonic EM field conveniently described by a
phasor notation (cf. (4.1)), the absorption coefficient
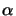 (x;t) can be related to the imaginary part
(x;t) can be related to the imaginary part 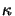 of the
complex-valued index of refraction
n bya
of the
complex-valued index of refraction
n bya
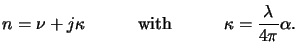 |
(5.3) |
The quantity 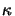 is commonly called the extinction coefficient of the
medium. By using the complex-valued index of refraction thus defined
the light absorption inside the medium while propagating through it is
implicitly accounted for. The above relation (5.3)
provides therefore an elegant way of describing both phenomena of field
propagation and absorption.
is commonly called the extinction coefficient of the
medium. By using the complex-valued index of refraction thus defined
the light absorption inside the medium while propagating through it is
implicitly accounted for. The above relation (5.3)
provides therefore an elegant way of describing both phenomena of field
propagation and absorption.
In case of a dilute solution the absorption coefficient
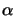 (x;t)
introduced in Lambert's law (5.1) is proportional to the
concentration
C(x;t) of the absorbing species, i.e.,
(x;t)
introduced in Lambert's law (5.1) is proportional to the
concentration
C(x;t) of the absorbing species, i.e.,
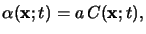 |
(5.4) |
which is commonly referred to as Beer's law [135].
This simple relation
starts to fail at high particle concentration as it is based
on the assumption of complete independence of the absorbing molecules.
If the particles get too close to each other they mutually influence each other.
Since any interaction depends on the concentration
C(x;t), the linear relation postulated by Beer's law in
(5.4) breaks down. Another apparent deviation
from (5.4) occurs if the real part 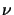 of the refraction index n
strongly depends on the concentration. Thus the validity
of Beer's law is not always guaranteed but should be checked over the
concentration range of interest.
of the refraction index n
strongly depends on the concentration. Thus the validity
of Beer's law is not always guaranteed but should be checked over the
concentration range of interest.
A simple extension of (5.4) applies to materials consisting of
multiple absorbing components. In such a situation the overall absorption
coefficient can be written as
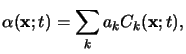 |
(5.5) |
provided that the independence also holds across the different absorbing
species. The basic results stated in (5.1)
to (5.5) will now be used for the modeling of the
two resist systems of interest.
Footnotes
- ... bya
- The spatial- and time-dependence is suppressed for the moment.




Next: 5.1.2 Modeling of Conventional
Up: 5.1 Exposure Kinetics
Previous: 5.1 Exposure Kinetics
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
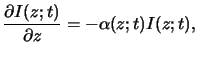
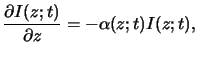
![]() (x;t) can be related to the imaginary part
(x;t) can be related to the imaginary part ![]() of the
complex-valued index of refraction
n bya
of the
complex-valued index of refraction
n bya
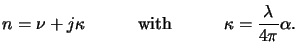
![]() (x;t)
introduced in Lambert's law (5.1) is proportional to the
concentration
C(x;t) of the absorbing species, i.e.,
(x;t)
introduced in Lambert's law (5.1) is proportional to the
concentration
C(x;t) of the absorbing species, i.e.,