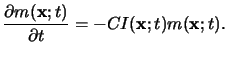5.1.2 Modeling of Conventional Resists

Following the Dill model [74] a typical conventional positive DQN resist consists of four major components, namely a base resin and solvent that both determine the structural properties, a photoactive compound (PAC) that is the light sensitive moiety, and exposure products generated by the reaction of the PAC with the exposing light. For more information about the decomposition of DQN resists see Section 2.6.2. Disregarding any chemical details the absorption coefficient of the photoresist can be written with (5.5) as

 

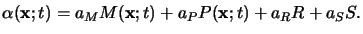$$\alpha(\mathbf{x};t) = a_{M}M(\mathbf{x};t) + a_PP(\mathbf{x};t) + a_RR + a_SS.$$ (5.6)

Here we have used the following notation: M stands for the PAC, P for the exposure products, R for the resin, and S for the solvents. Because of the stoichiometry of the exposure reaction, the exposure products P(x;t) are related to the PAC M(x;t) by

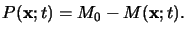$$P(\mathbf{x};t)=M_0-M(\mathbf{x};t).$$ (5.7)

Here M₀ denotes the initial PAC concentration. Using this relation the inhomogeneous terms in (5.6) can be separated and the absorption coefficient 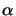$\alpha$(x;t) of the photoresist follows to

 

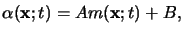$$\alpha(\mathbf{x};t) = A m(\mathbf{x};t) + B,$$ (5.8)

whereby the lower case letter m(x;t) refers to the absolute PAC concentration M(x;t) normalized by its initial concentration M₀, i.e.,

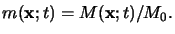$$m(\mathbf{x};t) = M(\mathbf{x};t)/M_0.$$ (5.9)

Hence the two constant parameters A and B are easily determined by comparison of (5.8) with (5.6) yielding

 

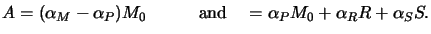$$A= (\alpha_M - \alpha_P) M_0 \quad\qquad\text{and}\quad\qquadB = \alpha_PM_0 + \alpha_RR + \alpha_SS.$$ (5.10)

The two quantities A and B make up the first two Dill photoresist parameters and are also called the bleachable and non-bleachable absorption coefficient of the photoresist, respectively. This terminology stems from the fact that the relation (5.8) describes the bleaching of the resist. Bleaching implies the decrease of the absorbance 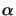$\alpha$(x;t) during exposure as the PAC decomposes and thus m(x;t) decreases. This phenomenon is of great importance because the resist becomes more transparent and therefore also deeper regions are exposed with sufficiently high light intensity.

What is missing now is the chemical modeling of the absorption process on an atomic level. For that the absorption process can be thought of as photons being absorbed by an atom or molecule causing an outer electron to be promoted to a higher energy state. The light energy thereby absorbed first weakens and finally breaks atomic bonds and thus stimulates the chemical conversion of the PAC M(x;t) into its exposure products P(x;t). Neglecting the intermediate excited state of the molecules and only considering the direct transition from the PAC to the products, i.e.,

 

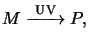$$M @>{\;\mathrm{UV}\;}>> P,$$ (5.11)

the rate equation for this basic reaction can be derived with the help of simple kinetic theory like the mass action law and writes to

 

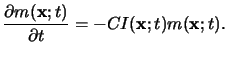$$\frac{\partial m(\mathbf{x};t)}{\partial t} = -C I(\mathbf{x};t) m(\mathbf{x};t).$$ (5.12)

Here C is the third Dill parameter of the resist describing the standard exposure rate, and I(x;t) is the absorbed light intensity. The relation simply postulates that the dissolution rate of the PAC is proportional to the absorbed light intensity and the momentarily available amount of the PAC. Most important, it shows the fundamental operation principle of the photoresist. As the absorbed light intensity I(x;t) depends on the aerial image I_i(x, y) that in its turn carries the mask pattern, the image of the mask is stored in a latent image m(x;t_exp) within the resist determining the chemical state after an exposure of duration t_exp.

The two relations (5.8) and (5.12) constitute the so-called Dill's `ABC'-model. The three parameters A, B, and C involved can be obtained by graphical analysis of measured data [74] or by fitting numerical simulation results to an entirely experimental curve [136,137,138]. Values can be found in the literature; however, every new resist has to be analyzed separately and the extracted values are kept strictly confidential by any IC manufacturer.