



Next: 5.1.4 Simulation Flow
Up: 5.1 Exposure Kinetics
Previous: 5.1.2 Modeling of Conventional
5.1.3 Modeling of Chemically Amplified Resists
The composition of chemically amplified photoresists was already described in
some detail in Section 2.6.4.
Typically they contain a polymer resin that is often ``blocked'' to inhibit
dissolution, a photoacid generator (PAG),
and possibly a crosslinking agent, a dye or any other additive. As the name
implies the PAG forms a strong acid when exposed to DUV light, i.e.,
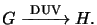 |
(5.13) |
Here G denotes the PAG and H stands for the generated acid. Due to the
stoichiometry of the reaction the generated acid concentration
H(x;t)
can be expressed by
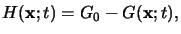 |
(5.14) |
whereby G0 refers to the initial PAG concentration.
Similar to (5.12) the dissolution of the PAG can be modeled by a
simple first-order reaction equation like
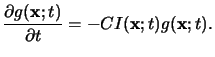 |
(5.15) |
Upper case letters again refer to absolute concentrations,
whereas the quantities normalized by the initial PAG concentration G0
are denoted by lower case letters. (5.15) shows that the
exposure of the resist now results in an acid latent image
g(x;t).
Subsequently a post-exposure bake has to thermally induce a second chemical
reaction that transfers the acid image to a solubility rate
modulated correspondingly (cf. Section 2.6.4).
From now on we restrict the discussion to the concept of deblocking the polymer
resin as it occurs in the case of a positive chemically amplified resist,
i.e., the originally high solubility of the resist is reduced.
Using
m(x;t) as the concentration of some reactive sites,
these sites are consumed according to the kinetics of some unknown order n
in
h(x;t) and of first-order in
m(x;t) [139].
Hence the reaction equation is given by
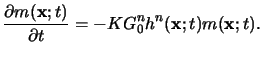 |
(5.16) |
The chemical amplification can best be understood by integrating
the two relations (5.15) and (5.16) over the
exposure time
texp and post-exposure bake time
tpeb,
respectively,
Note that for the second integration we have assumed a constant acid
concentration
h(x;texp) during the entire
post-exposure bake. Thus the PAG is modeled to act as an ideal catalyzer.
In reality the acid itself is also consumed by the reaction
(5.16) but at a much smaller rate than the reactive sites
m(x;t). Furthermore the acid will diffuse due to the elevated
temperature during the bake step. This means that the reaction
(5.16) has to be combined with a diffusion equation to account
for the motion of the acid. We will present some modeling aspects of this
topic in connection with the development simulation in Section 7.1.2.
However, an interpretation of the two relations given in (5.17)
already demonstrates the operation principle of chemical amplification.
In regions of high exposing light intensity, i.e., in the blank areas,
a high acid concentration resides so that
h(x;texp) 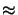 1.
Consequently only few reactive sites
m(x;tpeb)
1.
Consequently only few reactive sites
m(x;tpeb) 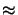 0
remain after the post-exposure bake. In regions of low exposing light
intensity, i.e., in the opaque areas, the contrary process occurs. Hence
the resist stores a positive image of the mask.
The amplification of the acid
h(x;texp) that results in
the enhanced final latent image
m(x;tpeb)
can be explained by rewriting the second relation of (5.17) like
0
remain after the post-exposure bake. In regions of low exposing light
intensity, i.e., in the opaque areas, the contrary process occurs. Hence
the resist stores a positive image of the mask.
The amplification of the acid
h(x;texp) that results in
the enhanced final latent image
m(x;tpeb)
can be explained by rewriting the second relation of (5.17) like
 |
(5.17) |
The quantity
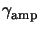 is called the lumped ``amplification''
constant as it describes the achievable amplification of the intermediate acid
image with respect to the final image.
is called the lumped ``amplification''
constant as it describes the achievable amplification of the intermediate acid
image with respect to the final image.




Next: 5.1.4 Simulation Flow
Up: 5.1 Exposure Kinetics
Previous: 5.1.2 Modeling of Conventional
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
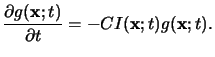
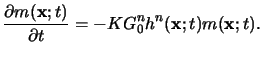
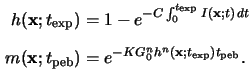
![]() 1.
Consequently only few reactive sites
m(x;tpeb)
1.
Consequently only few reactive sites
m(x;tpeb) ![]() 0
remain after the post-exposure bake. In regions of low exposing light
intensity, i.e., in the opaque areas, the contrary process occurs. Hence
the resist stores a positive image of the mask.
The amplification of the acid
h(x;texp) that results in
the enhanced final latent image
m(x;tpeb)
can be explained by rewriting the second relation of (5.17) like
0
remain after the post-exposure bake. In regions of low exposing light
intensity, i.e., in the opaque areas, the contrary process occurs. Hence
the resist stores a positive image of the mask.
The amplification of the acid
h(x;texp) that results in
the enhanced final latent image
m(x;tpeb)
can be explained by rewriting the second relation of (5.17) like