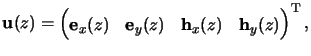Next: 6.3 Formulation of the
Up: 6.2 Lateral Discretization of
Previous: 6.2.5 Truncation of the
6.2.6 Vector-Matrix Notation
Any further considerations are much simplified by switching over to a
vector-matrix notation. For that we introduce the following four
NODE/4-dimensional vectors comprising the
(2Nx + 1) x (2Ny + 1)
Fourier coefficients of the four relevant field components:
Within each of these vectors the coefficients are arranged accordingly to
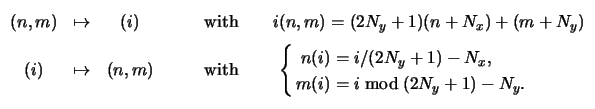 |
(6.22) |
The mapping is unique and invertible, i.e., any index pair (n, m) corresponds
to one unequivocal vector-entry i, and vice versa.
The same methodology can be applied to the coefficients of the ODE system
(6.22). Each of the eight sets
rnm, pq
 (z) and
gnm, pq
(z) and
gnm, pq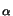
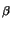 (z) with
(
(z) with
(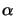
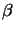 )
) 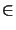 {(xx),(xy),(yx),(yy)}
is arranged in one
NODE/4 x NODE/4-matrix.
The ODE system can thus be written in the compact form
{(xx),(xy),(yx),(yy)}
is arranged in one
NODE/4 x NODE/4-matrix.
The ODE system can thus be written in the compact form
![$\displaystyle \frac{d}{dz} \begin{pmatrix}\mathbf{e}_x(z)\\ \mathbf{e}_y(z) \\ ...
...x(z)\\ \mathbf{e}_y(z) \\ [2pt] \mathbf{h}_x(z)\\ \mathbf{h}_y(z)\end{pmatrix}.$](img879.gif) |
(6.23) |
The overall shape of the system matrix reflects the fundamental structure of the
Maxwell equations since the derivative of the electric field depends only
on the derivative of the magnetic field and vice versa.
Comprising the four field coefficient vectors of (6.30)
to one
NODE-dimensional vector
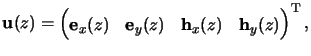 |
(6.24) |
we obtain the most compact and convenient formc
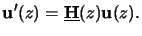 |
(6.25) |
Here the
NODE x NODE-dimensional system matrix
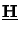 (z) follows from (6.34). Its
entries hij(z) are determined by the Fourier coefficients
(z) follows from (6.34). Its
entries hij(z) are determined by the Fourier coefficients
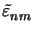 (z) and
(z) and
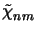 (z) of the permittivity and its reciprocal, respectively.
With the mapping (6.31) we obtain, e.g,
(z) of the permittivity and its reciprocal, respectively.
With the mapping (6.31) we obtain, e.g,
![$\displaystyle [\underline{\mathbf{H}}(z)]_{i+2{N_{\mathrm{ODE}}}/{4}, j+3{N_{\mathrm{ODE}}}/{4}} =[\underline{\mathbf{G}}^{xy}(z)]_{ij},\vspace*{-1ex}$](img885.gif) |
(6.26) |
whereby
1 i, j < NODE/4. The given example takes the
explicit form (c.f. (6.22))
i, j < NODE/4. The given example takes the
explicit form (c.f. (6.22))
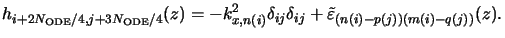 |
(6.27) |
Footnotes
- ... formc
- A prime as superscript
denotes derivation with respect to the independent variable that is the vertical
coordinate z in our case.




Next: 6.3 Formulation of the
Up: 6.2 Lateral Discretization of
Previous: 6.2.5 Truncation of the
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
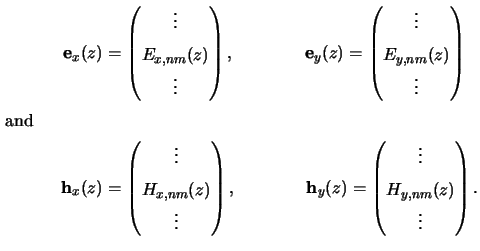
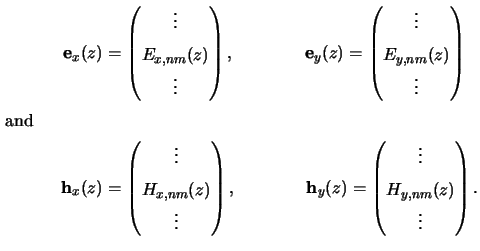
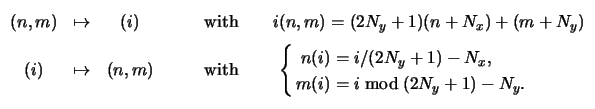
![]()
![]() (z) and
gnm, pq
(z) and
gnm, pq![]()
![]() (z) with
(
(z) with
(![]()
![]() )
) ![]() {(xx),(xy),(yx),(yy)}
is arranged in one
NODE/4 x NODE/4-matrix.
The ODE system can thus be written in the compact form
{(xx),(xy),(yx),(yy)}
is arranged in one
NODE/4 x NODE/4-matrix.
The ODE system can thus be written in the compact form
![$\displaystyle \frac{d}{dz} \begin{pmatrix}\mathbf{e}_x(z)\\ \mathbf{e}_y(z) \\ ...
...x(z)\\ \mathbf{e}_y(z) \\ [2pt] \mathbf{h}_x(z)\\ \mathbf{h}_y(z)\end{pmatrix}.$](img879.gif)