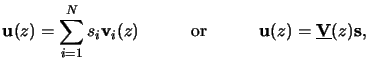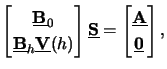Next: 6.4.3.1 Shooting with Reduced
Up: 6.4.3 Shooting Method
Previous: 6.4.3 Shooting Method
Single shooting is based on the principle of
superposition valid for linear ODEs,e i.e., any linear
combination
v(z) = 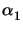 v1(z) +
v1(z) + 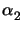 v2(z)
of two individual solutions
v1(z) and
v2(z) satisfying
the ODE
v
v2(z)
of two individual solutions
v1(z) and
v2(z) satisfying
the ODE
v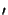 (z) =
(z) = 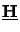 (z)v(z) is again
a solution of it. The basic theory of ODEs states that an N-dimensional ODE
system has exactly N linearly independent solution vectors
vi(z)
with
i = 1,..., N [200, pp. 85-93]. The BCs can be chosen arbitrarily
provided that the vectors
vi(z) are linearly
independent and thus span the whole N-dimensional vector space
(z)v(z) is again
a solution of it. The basic theory of ODEs states that an N-dimensional ODE
system has exactly N linearly independent solution vectors
vi(z)
with
i = 1,..., N [200, pp. 85-93]. The BCs can be chosen arbitrarily
provided that the vectors
vi(z) are linearly
independent and thus span the whole N-dimensional vector space
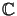 N.
By taking the unit vectors
ei, i.e.,
[ei]j =
N.
By taking the unit vectors
ei, i.e.,
[ei]j = 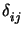 ,
as initial values at one boundary point, e.g., at z = 0, the
obtained solutions
vi(z) are called fundamental solutions,
,
as initial values at one boundary point, e.g., at z = 0, the
obtained solutions
vi(z) are called fundamental solutions,
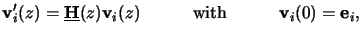 |
(6.36) |
that are arranged in the N x N-dimensional
fundamental solution matrix
V(z). The solution
u(z)
of any first-order, N-dimensional BVP can be represented by a
specific superposition of the fundamental solutions, i.e.,
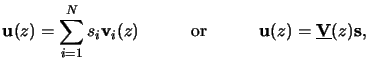 |
(6.37) |
with
 |
(6.38) |
The coefficients si have to be chosen so that the imposed BCs are satisfied,
i.e., in our case they take the form (cf. (6.51))
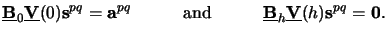 |
(6.39) |
These two equations build up a linear algebraic system. Due to the multiple
excitation vectors
apq we obtain an algebraic equation with Ns
right-hand sides and thus Ns coefficient vectors
spq, i.e.,
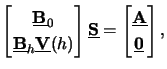 |
(6.40) |
whereby all the Ns vectors
apq and
spq are
grouped together in the two matrices
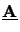 and
and
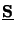 ,
respectively (cf. (6.54)). Note that
,
respectively (cf. (6.54)). Note that
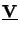 (0) =
(0) = 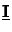 has already been inserted for the fundamental
solutions at z = 0. (6.59) can
be efficiently solved with LU-factorization [202, pp. 94-104] to
obtain simultaneously
all the coefficients
spq looked for. With them the
solution
has already been inserted for the fundamental
solutions at z = 0. (6.59) can
be efficiently solved with LU-factorization [202, pp. 94-104] to
obtain simultaneously
all the coefficients
spq looked for. With them the
solution
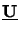 (z) can directly be calculated from (6.56)
if the complete fundamental solution matrix
(z) can directly be calculated from (6.56)
if the complete fundamental solution matrix
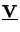 (z) is stored for all
interesting vertical positions. Otherwise the initial values at z = 0
are simply given by
(z) is stored for all
interesting vertical positions. Otherwise the initial values at z = 0
are simply given by
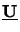 (0) =
(0) = 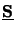 since
since
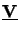 (0) =
(0) = 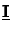 and the IVP thus obtained can easily be integrated.
An algorithm implementing the above procedure is described in
Table 6.2. As already mentioned this algorithm suffers
from potential instabilities [200, pp. 137-143] and has thus to be
further refined for our problem.
and the IVP thus obtained can easily be integrated.
An algorithm implementing the above procedure is described in
Table 6.2. As already mentioned this algorithm suffers
from potential instabilities [200, pp. 137-143] and has thus to be
further refined for our problem.
Table 6.2:
Algorithm for single shooting.
 |
Footnotes
- ... ODEs,e
- This does
not mean that shooting is restricted to linear ODEs. In the
linear case, however, the theory can be presented in a very compact and
elegant way, whereas in the nonlinear case the treatment is more complicated
and additional steps are required. Since our problem is linear we restrict
the discussion to this simpler situation.




Next: 6.4.3.1 Shooting with Reduced
Up: 6.4.3 Shooting Method
Previous: 6.4.3 Shooting Method
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17