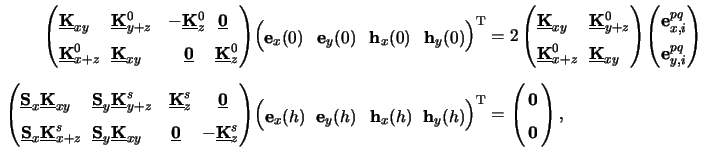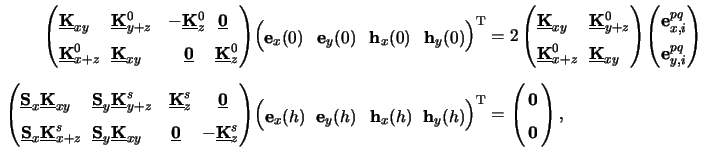Next: 6.4 Vertical Discretization of
Up: 6.3 Formulation of the
Previous: 6.3.2 Resist/Substrate Interface
6.3.3 Vector-Matrix Notation
In Section 6.2.6 we introduced a vector-matrix notation
to achieve a compact form for the ODE system.
The notation is governed by the convention (6.30)
combined with the index-mapping of (6.31). Using this notation
the BCs (6.40) and (6.47)
at z = 0 and z = h, respectively, take the form
whereby all
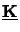 -matrices as well as the two
-matrices as well as the two
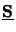 -matrices
are diagonal with dimension
NODE x NODE.
For example,
-matrices
are diagonal with dimension
NODE x NODE.
For example,
![$\displaystyle [\underline{\mathbf{K}}^s_{x+z}]_{ij}=\left(k^2_{x,n(i)}+k^2_{z,s...
...qquad\text{and}\qquad[\underline{\mathbf{S}}_{x}]_{ij} = s_{x,n(i)}\delta_{ij}.$](img915.gif) |
(6.31) |
Note that the diagonal property of the matrices reflects the mutual
independence of the BCs of different harmonic frequencies (n, m).
Similarly, to the transition from (6.32) to (6.34)
we comprise the individual coefficient vectors to one common vector
u(z) (cf. (6.33)) and can thus further
condense (6.49) to
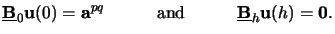 |
(6.32) |
The two boundary matrices
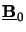 and
and
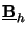 are both of dimension
NODE/2 x NODE, whereas the excitation vectors
apq and
0 are of dimension
NODE/2.
At the upper interface at z = 0 a different excitation vector
apq
occurs for each coherent source point (p, q). The simultaneous treatment
of multiple BCs will be described in
Section 6.4.3 which is one of the major advantages of the
proposed implementation of the differential method. Furthermore it is
worth mentioning that the excitation vector at the lower interface z = h
vanishes, i.e., we have the zero-vector
0, which reflects that only
outgoing waves occur in the substrate due to the assumption
of an infinitely extended substrate (cf. Fig. 6.1).
are both of dimension
NODE/2 x NODE, whereas the excitation vectors
apq and
0 are of dimension
NODE/2.
At the upper interface at z = 0 a different excitation vector
apq
occurs for each coherent source point (p, q). The simultaneous treatment
of multiple BCs will be described in
Section 6.4.3 which is one of the major advantages of the
proposed implementation of the differential method. Furthermore it is
worth mentioning that the excitation vector at the lower interface z = h
vanishes, i.e., we have the zero-vector
0, which reflects that only
outgoing waves occur in the substrate due to the assumption
of an infinitely extended substrate (cf. Fig. 6.1).




Next: 6.4 Vertical Discretization of
Up: 6.3 Formulation of the
Previous: 6.3.2 Resist/Substrate Interface
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17