



Next: 5.2.2 Materialabhängigkeit
Up: 5.2 Effektive Masse
Previous: 5.2 Effektive Masse
5.2.1 Die 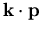 Methode
Methode
Die 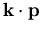 Methode ist eine Anwendung der stationären Störungstheorie der Quantenmechanik .
Als solche gestattet sie die Berechnung der Bandstruktur in der Umgebung der Bandkanten im Gegensatz zu anderen Methoden, welche die Bandstruktur in der ganzen Brillouinzone beschreiben (``tight-binding'', LCAO, ``pseudopotentials'').
Im Vergleich zu diesen ab initio Rechnungen ist sie relativ einfach, benötigt allerdings Eigenschaften der wirklichen Bandstruktur als Eingangsparameter.
Dieses im Zuge des Rechenvorgangs relativ späte Einfließen experimenteller Daten hat aber andererseits den Vorteil, dadurch oft bessere Übereinstimmung mit der Realität zu erzielen.
Da man ohnedies meist nur an der Charakteristik in der Nähe der Bandextrema interessiert ist (EMA), ist die Anwendung der
Methode ist eine Anwendung der stationären Störungstheorie der Quantenmechanik .
Als solche gestattet sie die Berechnung der Bandstruktur in der Umgebung der Bandkanten im Gegensatz zu anderen Methoden, welche die Bandstruktur in der ganzen Brillouinzone beschreiben (``tight-binding'', LCAO, ``pseudopotentials'').
Im Vergleich zu diesen ab initio Rechnungen ist sie relativ einfach, benötigt allerdings Eigenschaften der wirklichen Bandstruktur als Eingangsparameter.
Dieses im Zuge des Rechenvorgangs relativ späte Einfließen experimenteller Daten hat aber andererseits den Vorteil, dadurch oft bessere Übereinstimmung mit der Realität zu erzielen.
Da man ohnedies meist nur an der Charakteristik in der Nähe der Bandextrema interessiert ist (EMA), ist die Anwendung der 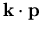 Methode sehr populär und instruktiv, gibt sie doch anschauliche Resultate für die experimentell feststellbaren Zusammenhänge.
In der Folge ist zunächst die stationäre Störungstheorie (Perturbationsmethode) der Quantenmechanik kurz rekapituliert [145].
Methode sehr populär und instruktiv, gibt sie doch anschauliche Resultate für die experimentell feststellbaren Zusammenhänge.
In der Folge ist zunächst die stationäre Störungstheorie (Perturbationsmethode) der Quantenmechanik kurz rekapituliert [145].
Ausgehend von der bekannten Lösung eines Eigenwertproblems des Operators 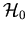
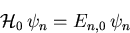 |
(5.26) |
für die Eigenwerte En,0 und Eigenzustände 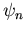 erlaubt sie, in sehr eleganter Weise die Lösung eines schwach gestörten Systems näherungsweise zu ermitteln. Der Operator des gestörten Systems sei
erlaubt sie, in sehr eleganter Weise die Lösung eines schwach gestörten Systems näherungsweise zu ermitteln. Der Operator des gestörten Systems sei
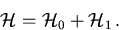 |
(5.27) |
Die Eigenwerte des gestörten Systems lassen sich in eine Reihe entwickeln,
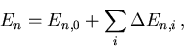 |
(5.28) |
wobei die Korrekturen 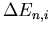 nur Funktionen der Eigenwerte und Eigenzustände des ungestörten Ausgangssystem sind. i ist die Ordnung der Störungsrechnung. Der Korrekturterm erster Ordnung für den nicht entarteten Eigenwert En ist das Matrixelement des Störoperators,
nur Funktionen der Eigenwerte und Eigenzustände des ungestörten Ausgangssystem sind. i ist die Ordnung der Störungsrechnung. Der Korrekturterm erster Ordnung für den nicht entarteten Eigenwert En ist das Matrixelement des Störoperators,
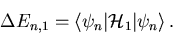 |
(5.29) |
Die verwendete Dirac Notation des Matrixelements steht für
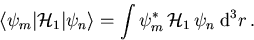 |
(5.30) |
Der Korrekturterm zweiter Ordnung hat die Form
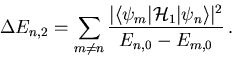 |
(5.31) |
In analoger Form gibt es auch eine Entwicklung für die Eigenzustände des gestörten Systems.
Die Perturbationsmethode zweiter Ordnung wird nun zur Berechnung der Bandstruktur, also der Eigenwerte der Schrödingergleichung für die Kristallelektronen, angewendet.
Betrachtet man die Schrödingergleichung in der zeitunabhängigen Form,
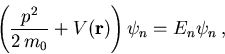 |
(5.32) |
so setzt sich der Hamilton Operator 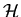 aus dem Impulsoperator
aus dem Impulsoperator 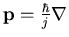 (kinetische Energie) und dem Operator der potentiellen Energie
(kinetische Energie) und dem Operator der potentiellen Energie 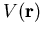 zusammen, n ist der Bandindex.
Setzt man für die Eigenzustände Blochfunktionen (Abschnitt 3.2) an,
zusammen, n ist der Bandindex.
Setzt man für die Eigenzustände Blochfunktionen (Abschnitt 3.2) an,
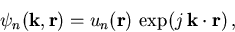 |
(5.33) |
so erhält man
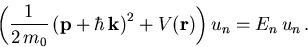 |
(5.34) |
Für einen bestimmten Wert 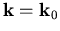 , einfacherweise
, einfacherweise 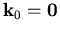 (
(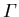 ), kennt man die Lösung von
), kennt man die Lösung von
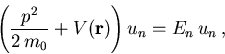 |
(5.35) |
also die Bandstruktur 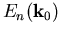 . Dann ist der Störoperator gegeben durch
. Dann ist der Störoperator gegeben durch
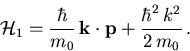 |
(5.36) |
Der erste Term des Störoperators ist linear in 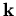 , er ist auch der Grund für die Namensbezeichnung dieser Methode.
Die Korrektur erster Ordnung (5.29) liefert
, er ist auch der Grund für die Namensbezeichnung dieser Methode.
Die Korrektur erster Ordnung (5.29) liefert
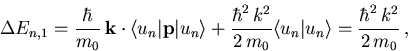 |
(5.37) |
also nur quadratische Anteile in k, wobei die Tatsache des relativen Extremums und die Normierung von 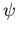 benützt wurden
benützt wurden![[*]](foot_motif.gif) .
Die Korrektur zweiter Ordnung (5.31) mit Potenzen bis k2 lautet
.
Die Korrektur zweiter Ordnung (5.31) mit Potenzen bis k2 lautet
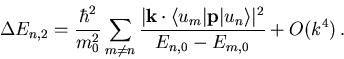 |
(5.38) |
Die so gefundene Beziehung für 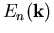 bis zur zweiten Potenz in k ist die Bandstruktur für
bis zur zweiten Potenz in k ist die Bandstruktur für 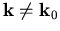 in der Umgebung des Extremums
in der Umgebung des Extremums 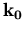
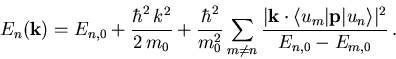 |
(5.39) |
Sie erlaubt es, den Tensor der effektiven Masse des Bandes n zu bestimmen. Aus dem Vergleich des Ergebnisses (5.39) mit der allgemeinen Darstellung der analytischen Bandstruktur in der EMA
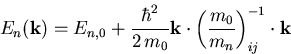 |
(5.40) |
folgt also
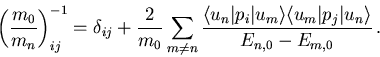 |
(5.41) |
Zur Bestimmung der effektiven Masse ist also die Kenntnis der Bandenergien En,0 und der Impulsmatrixelemente 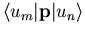 (``momentum matrix element'') und damit der Wellenfunktionen un nötig. Aufgrund der Symmetrie kubischer HL sind allerdings nur wenige dieser auch Interbandmatrixelemente genannten Ausdrücke von Null verschieden.
Als wichtigstes Beispiel wird die effektive Masse des Leitungsbands direkter HL betrachtet.
Die LB Zustände bei
(``momentum matrix element'') und damit der Wellenfunktionen un nötig. Aufgrund der Symmetrie kubischer HL sind allerdings nur wenige dieser auch Interbandmatrixelemente genannten Ausdrücke von Null verschieden.
Als wichtigstes Beispiel wird die effektive Masse des Leitungsbands direkter HL betrachtet.
Die LB Zustände bei 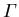 sind sphärisch symmetrisch (s-Symmetrie), die VB Zustände weisen Vorzugsrichtungen entlang der Koordinatenachsen auf (p-Symmetrie).
Die einzigen nicht verschwindenden Matrixelemente sind von der Form
sind sphärisch symmetrisch (s-Symmetrie), die VB Zustände weisen Vorzugsrichtungen entlang der Koordinatenachsen auf (p-Symmetrie).
Die einzigen nicht verschwindenden Matrixelemente sind von der Form 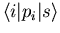 . Zusätzlich gilt
. Zusätzlich gilt 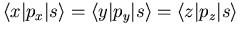 , das heißt die Bestimmung der Wechselwirkung zwischen dem ersten LB und dem VB bei
, das heißt die Bestimmung der Wechselwirkung zwischen dem ersten LB und dem VB bei 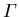 reduziert sich auf ein Matrixelement.
Meist wird dieses kurz als das LB-VB Matrixelement bezeichnet und in der Form einer Wechselwirkungsenergie
reduziert sich auf ein Matrixelement.
Meist wird dieses kurz als das LB-VB Matrixelement bezeichnet und in der Form einer Wechselwirkungsenergie
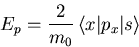 |
(5.42) |
verwendet. Ep ist dann eine einfache Materialkonstante.
Offen ist nun noch die Frage, wieviele Bänder zur Bestimmung der Masse des betrachteten LB nötig sind.
Einerseits sind die Matrixelemente zwischen dem ersten und den nächsthöheren LB wesentlich kleiner als Ep [85].
Aufgrund der Abhängigkeit von (5.41) von den Bandabständen En-Em sieht man andererseits, daß energetisch nähere Bänder stärkeren Einfluß haben. Unter Beachtung der Bandstruktur von III-V HL (vgl. Abbildung 3.5) erkennt man weiters, daß zur Bestimmung von 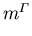 das Valenzband ausreichend ist. Höhere LB sind im allgemeinen vernachlässigbar, liegen sie doch bei
das Valenzband ausreichend ist. Höhere LB sind im allgemeinen vernachlässigbar, liegen sie doch bei 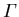 um den Faktor 3 weiter entfernt als das VB.
Aus der Anzahl der berücksichtigten Bänder leitet sich auch die genauere Klassifikation der Methode ab. Im Fall der Verwendung von erstem LB und hh, lh und so VB spricht man von einer ``4-Band
um den Faktor 3 weiter entfernt als das VB.
Aus der Anzahl der berücksichtigten Bänder leitet sich auch die genauere Klassifikation der Methode ab. Im Fall der Verwendung von erstem LB und hh, lh und so VB spricht man von einer ``4-Band 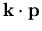 Rechnung''.
Aus dieser folgt also der Ausdruck für die effektive Masse in Einheiten der freien Elektronenmasse m0
Rechnung''.
Aus dieser folgt also der Ausdruck für die effektive Masse in Einheiten der freien Elektronenmasse m0
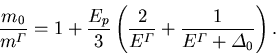 |
(5.43) |
Man erkennt, daß die direkte Bandlücke und die effektive Masse stark gekoppelt sind. Je kleiner die Bandlücke desto kleiner ist auch die Masse (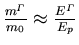 ).
).




Next: 5.2.2 Materialabhängigkeit
Up: 5.2 Effektive Masse
Previous: 5.2 Effektive Masse
Christian Koepf
1997-11-11
![]()
![[*]](foot_motif.gif) .
Die Korrektur zweiter Ordnung (5.31) mit Potenzen bis k2 lautet
.
Die Korrektur zweiter Ordnung (5.31) mit Potenzen bis k2 lautet
![]() (``momentum matrix element'') und damit der Wellenfunktionen un nötig. Aufgrund der Symmetrie kubischer HL sind allerdings nur wenige dieser auch Interbandmatrixelemente genannten Ausdrücke von Null verschieden.
Als wichtigstes Beispiel wird die effektive Masse des Leitungsbands direkter HL betrachtet.
Die LB Zustände bei
(``momentum matrix element'') und damit der Wellenfunktionen un nötig. Aufgrund der Symmetrie kubischer HL sind allerdings nur wenige dieser auch Interbandmatrixelemente genannten Ausdrücke von Null verschieden.
Als wichtigstes Beispiel wird die effektive Masse des Leitungsbands direkter HL betrachtet.
Die LB Zustände bei ![]() sind sphärisch symmetrisch (s-Symmetrie), die VB Zustände weisen Vorzugsrichtungen entlang der Koordinatenachsen auf (p-Symmetrie).
Die einzigen nicht verschwindenden Matrixelemente sind von der Form
sind sphärisch symmetrisch (s-Symmetrie), die VB Zustände weisen Vorzugsrichtungen entlang der Koordinatenachsen auf (p-Symmetrie).
Die einzigen nicht verschwindenden Matrixelemente sind von der Form ![]() . Zusätzlich gilt
. Zusätzlich gilt ![]() , das heißt die Bestimmung der Wechselwirkung zwischen dem ersten LB und dem VB bei
, das heißt die Bestimmung der Wechselwirkung zwischen dem ersten LB und dem VB bei ![]() reduziert sich auf ein Matrixelement.
Meist wird dieses kurz als das LB-VB Matrixelement bezeichnet und in der Form einer Wechselwirkungsenergie
reduziert sich auf ein Matrixelement.
Meist wird dieses kurz als das LB-VB Matrixelement bezeichnet und in der Form einer Wechselwirkungsenergie
![]() das Valenzband ausreichend ist. Höhere LB sind im allgemeinen vernachlässigbar, liegen sie doch bei
das Valenzband ausreichend ist. Höhere LB sind im allgemeinen vernachlässigbar, liegen sie doch bei ![]() um den Faktor 3 weiter entfernt als das VB.
Aus der Anzahl der berücksichtigten Bänder leitet sich auch die genauere Klassifikation der Methode ab. Im Fall der Verwendung von erstem LB und hh, lh und so VB spricht man von einer ``4-Band
um den Faktor 3 weiter entfernt als das VB.
Aus der Anzahl der berücksichtigten Bänder leitet sich auch die genauere Klassifikation der Methode ab. Im Fall der Verwendung von erstem LB und hh, lh und so VB spricht man von einer ``4-Band ![]() Rechnung''.
Aus dieser folgt also der Ausdruck für die effektive Masse in Einheiten der freien Elektronenmasse m0
Rechnung''.
Aus dieser folgt also der Ausdruck für die effektive Masse in Einheiten der freien Elektronenmasse m0