5.2.1 Wahl der Selbststreurate




Next: 5.2.2 Wahl der freien
Up: 5.2 Ein verbesserter Selbststreualgorithmus
Previous: 5.2 Ein verbesserter Selbststreualgorithmus
Den Ausgangspunkt für den in dieser Dissertation entwickelten Algorithmus
bildet die Überlegung, daß die Selbststreurate nicht unbedingt dazu
verwendet werden muß, die Integralgleichung 4.35 in die
einfache Gleichung 5.2 überzuführen, die ja eine
Gleichung 1.Grades in 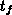 ist.
Es kann auch eine etwas komplizierte Gleichung zugelassen werden.
Sie sollte aber aus Effizienzgründen noch analytisch lösbar sein.
Verglichen mit stückweise konstantem
ist.
Es kann auch eine etwas komplizierte Gleichung zugelassen werden.
Sie sollte aber aus Effizienzgründen noch analytisch lösbar sein.
Verglichen mit stückweise konstantem 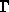 sollte die Zulassung einer
einfachen
sollte die Zulassung einer
einfachen 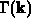 -Abhängigkeit es ermöglichen,
eine bessere einhüllende Funktion zu finden und auf diese Weise die
Selbststreuprozesse zu reduzieren.
-Abhängigkeit es ermöglichen,
eine bessere einhüllende Funktion zu finden und auf diese Weise die
Selbststreuprozesse zu reduzieren.
In Abschnitt 3.2.1 wurde gezeigt, daß für die
verwendete Diskretisierung der Wellenvektor linear mit der Zeit variiert.
Entlang einer Trajektorie unterliegt also der Skalar
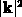 und die dazu proportionale
Größe
und die dazu proportionale
Größe 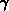 einer quadratischen Zeitentwicklung.
einer quadratischen Zeitentwicklung.
Um von einem konstantem 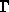 abzugehen, liegt es nahe,
abzugehen, liegt es nahe,
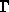 als eine lineare Funktion in
als eine lineare Funktion in 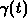 anzusetzen
anzusetzen
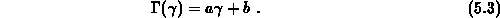
Da 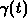 ein quadratisches Polynom in der Zeit ist, ergibt die
Zeitintegration von
ein quadratisches Polynom in der Zeit ist, ergibt die
Zeitintegration von 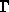 ein Polynom 3.Grades. Diese kubische Gleichung
kann zur Bestimmung der Flugdauer direkt gelöst werden.
Ein quadratisches Polynom in
ein Polynom 3.Grades. Diese kubische Gleichung
kann zur Bestimmung der Flugdauer direkt gelöst werden.
Ein quadratisches Polynom in 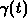 würde zwar die Erzeugung einer
noch besseren Einhüllenden gestatten, jedoch würde die resultierende
Integralgleichung 5.Ordnung in der Flugzeit sein. Der Rechenaufwand
für die numerische Lösung
dieser Gleichung würde die zusätzliche Einsparung von
Selbststreuprozessen nicht rechtfertigen.
würde zwar die Erzeugung einer
noch besseren Einhüllenden gestatten, jedoch würde die resultierende
Integralgleichung 5.Ordnung in der Flugzeit sein. Der Rechenaufwand
für die numerische Lösung
dieser Gleichung würde die zusätzliche Einsparung von
Selbststreuprozessen nicht rechtfertigen.
Setzt man in den Ansatz 5.3 die Zeitabhängigkeit von
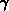 entsprechend Gleichung 3.32 ein, so wird
entsprechend Gleichung 3.32 ein, so wird
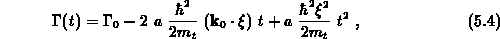
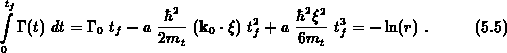
Für den Fall, daß das elektrische Feld verschwindet, bleibt der
Wellenvektor konstant und die obige Gleichung reduziert sich zu
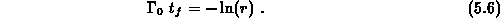
Für die Koeffizienten der kubischen Gleichung sollen folgende
Bezeichnungen verwendet werden:
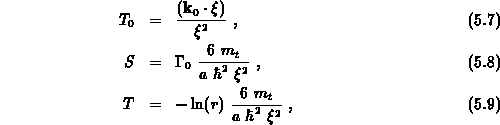
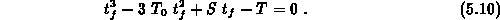
Durch die Substitution 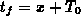 gelangt man zu der reduzierten
Gleichung
gelangt man zu der reduzierten
Gleichung
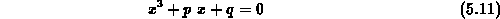
mit den Koeffizienten
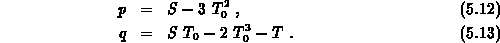
Das Lösungsverhalten der kubischen Gleichung hängt vom Vorzeichen
der Diskriminante
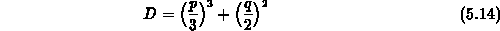
ab. Falls 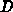 positiv ist, existieren genau eine reelle und zwei konjugiert
komplexe Lösungen.
positiv ist, existieren genau eine reelle und zwei konjugiert
komplexe Lösungen.
Im folgenden wird eine hinreichende Bedingung für 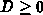 abgeleitet.
Der zweite Summand in Gleichung 5.14 ist unabhängig vom Vorzeichen
von
abgeleitet.
Der zweite Summand in Gleichung 5.14 ist unabhängig vom Vorzeichen
von 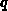 immer positiv. Also genügt es zu zeigen, daß
immer positiv. Also genügt es zu zeigen, daß 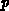 positiv ist,
positiv ist,
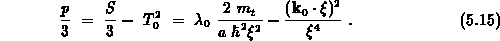
Mit Hilfe der Ungleichung
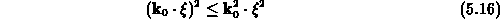
ergibt sich nach kurzer Zwischenrechnung die Bedingung
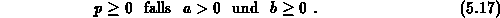
Das bedeutet, daß die lineare Funktion in der Gleichung 5.3 einen
positiven Ordinatenabschnitt und eine positive Steigung besitzt.
Die in dieser Arbeit verwendete totale Streurate 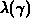 ist monoton
steigend in
ist monoton
steigend in 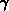 . Es hat sich herausgestellt,
daß vorteilhafte obere Begrenzungsfunktionen der Bedingung für positive
Diskriminante genügen (vergleiche Abbildung 5.2).
Es kann daher im Programm a priori davon ausgegangen werden, daß die
Gleichung genau eine reelle Lösung besitzt. Aus der Aufgabenstellung, ein
Integral über einen positiven Integrand zu berechnen, bis der
positive Wert
. Es hat sich herausgestellt,
daß vorteilhafte obere Begrenzungsfunktionen der Bedingung für positive
Diskriminante genügen (vergleiche Abbildung 5.2).
Es kann daher im Programm a priori davon ausgegangen werden, daß die
Gleichung genau eine reelle Lösung besitzt. Aus der Aufgabenstellung, ein
Integral über einen positiven Integrand zu berechnen, bis der
positive Wert 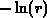 erreicht wird, folgt, daß die einzige reelle
Lösung auch positiv sein muß. Ohne vorherige Fallunterscheidung kann daher
die freie Flugdauer direkt durch die Formel von Cardano
[8]
erreicht wird, folgt, daß die einzige reelle
Lösung auch positiv sein muß. Ohne vorherige Fallunterscheidung kann daher
die freie Flugdauer direkt durch die Formel von Cardano
[8]
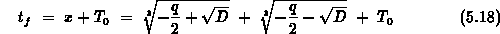
erhalten werden.
Im Programm wird nur die Vorbedingung
entsprechend Gleichung 5.17 überprüft,
eine Abfrage auf 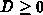 und
und 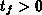 während der Simulation kann
unterbleiben.
während der Simulation kann
unterbleiben.
Liegt hingegen eine physikalische Streurate vor, für deren Einhüllende
auch abfallende Geraden verwendet werden, ist eine genaue Fallunterscheidung
unbedingt erforderlich. Es können dann auch drei reelle Lösungen auftreten,
wovon auf Grund der Problemstellung aber
mindestens eine positiv ist.




Next: 5.2.2 Wahl der freien
Up: 5.2 Ein verbesserter Selbststreualgorithmus
Previous: 5.2 Ein verbesserter Selbststreualgorithmus
Martin Stiftinger
Wed Oct 12 11:59:33 MET 1994
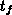 ist.
Es kann auch eine etwas komplizierte Gleichung zugelassen werden.
Sie sollte aber aus Effizienzgründen noch analytisch lösbar sein.
Verglichen mit stückweise konstantem
ist.
Es kann auch eine etwas komplizierte Gleichung zugelassen werden.
Sie sollte aber aus Effizienzgründen noch analytisch lösbar sein.
Verglichen mit stückweise konstantem 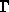 sollte die Zulassung einer
einfachen
sollte die Zulassung einer
einfachen 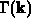 -Abhängigkeit es ermöglichen,
eine bessere einhüllende Funktion zu finden und auf diese Weise die
Selbststreuprozesse zu reduzieren.
-Abhängigkeit es ermöglichen,
eine bessere einhüllende Funktion zu finden und auf diese Weise die
Selbststreuprozesse zu reduzieren.




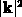 und die dazu proportionale
Größe
und die dazu proportionale
Größe 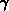 einer quadratischen Zeitentwicklung.
einer quadratischen Zeitentwicklung.
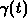 anzusetzen
anzusetzen
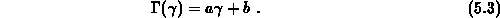
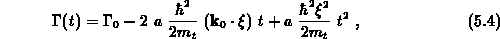
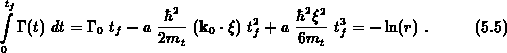
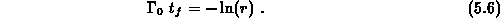
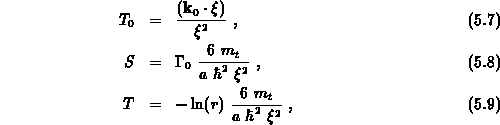
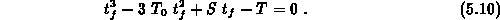
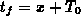 gelangt man zu der reduzierten
Gleichung
gelangt man zu der reduzierten
Gleichung
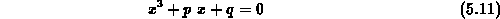
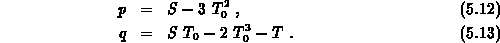
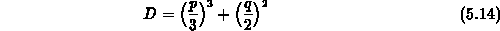
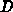 positiv ist, existieren genau eine reelle und zwei konjugiert
komplexe Lösungen.
positiv ist, existieren genau eine reelle und zwei konjugiert
komplexe Lösungen.
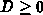 abgeleitet.
Der zweite Summand in Gleichung
abgeleitet.
Der zweite Summand in Gleichung 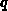 immer positiv. Also genügt es zu zeigen, daß
immer positiv. Also genügt es zu zeigen, daß 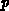 positiv ist,
positiv ist,
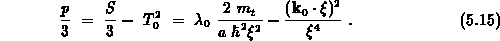
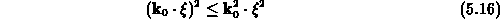
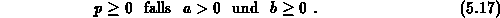
 ist monoton
steigend in
ist monoton
steigend in  erreicht wird, folgt, daß die einzige reelle
Lösung auch positiv sein muß. Ohne vorherige Fallunterscheidung kann daher
die freie Flugdauer direkt durch die Formel von Cardano
erreicht wird, folgt, daß die einzige reelle
Lösung auch positiv sein muß. Ohne vorherige Fallunterscheidung kann daher
die freie Flugdauer direkt durch die Formel von Cardano
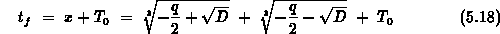
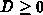 und
und 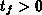 während der Simulation kann
unterbleiben.
während der Simulation kann
unterbleiben.