4.4 Results and Discussion

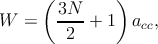
In this section, the energy dispersion relation and the wave functions for the approximated discrete wavenumbers θ are evaluated and compared against exact numerical calculations. Eq. 4.28 is employed to give the wave functions and energy dispersions from Eq. 4.12 and Eq. 4.18, respectively. Based on the structure depicted in Fig. 4.1, the width of a zigzag nanoribbon is given by

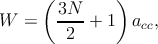(4.33)

where a_cc = 1.42 Å is the carbon-carbon bond length in graphene. For ZGNRs with a width below 50nm, indices in the range 6 to 235 have to be considered. In this range of indices the wave functions and the energy dispersion have been evaluated. It should be noted that structures wider than 50nm are also evaluated and the results show excellent agreement with those obtained from numerical simulation. Fig. 4.6 shows several wave functions for 125-ZGNR evaluated from two approximations proposed. As can be seen, the wave functions obtained by Eq. 4.28 are matched very well with the numerical calculations. The dispersion relation of some subbands for 125-ZGNR are shown in Fig. 4.7. Similar to the wave functions, the dispersion relations obtained by θ from Eq. 4.28, show well agreement with the numerical results.

An important conclusion that one can draw from these results is that the analytical approximation of θ presented in Eq. 4.28 is more accurate than the solution obtained by using a curve fitted θ, see Fig. 4.6 and Fig. 4.7. Also, the accuracy of the analytical method increases as the ZGNR index increases (see the energy dispersions for 6-ZGNR and 19-ZGNR in Fig. 4.4 and 125-ZGNR in Fig. 4.7).

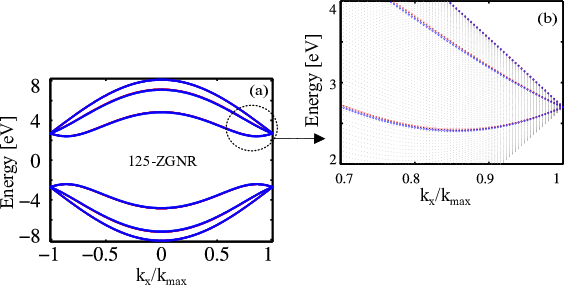
As can be see in Fig. 4.2, this increase in accuracy is due to the fact that θ is relatively independent of changes in the wave-vector (k_x) for large values of N.

In order to investigate the applicability of the proposed models, the optical matrix elements are derived analytically based on our models in 4.3. To evaluate the transition rules, we can also investigate the symmetry of the transition matrix element in Eq. 3.23. If the symmetry of this element spans the totally symmetric representation of the point group to which the unit cell belongs, then its value is not zero and the transition is allowed. Otherwise, the transition is forbidden. Assuming a uniform potential profile across the ribbon’s width, the subbands’ wave functions are either symmetric or antisymmetric along the y direction.

Considering the wave functions for 6-ZGNR and 19-ZGNR (Fig. 4.5), subbands corresponding to odd indices are symmetric, while those corresponding to even indices are antisymmetric. Therefore, the momentum matrix elements are non zero for transitions from the symmetric (antisymmetric) to the symmetric (antisymmetric) wave functions. This transition rule results in transitions from subbands with odd (even) to odd (even) indices in ZGNRs, [151] which confirms the result obtained from our analytical derivation of the wave functions and momentum matrix elements.

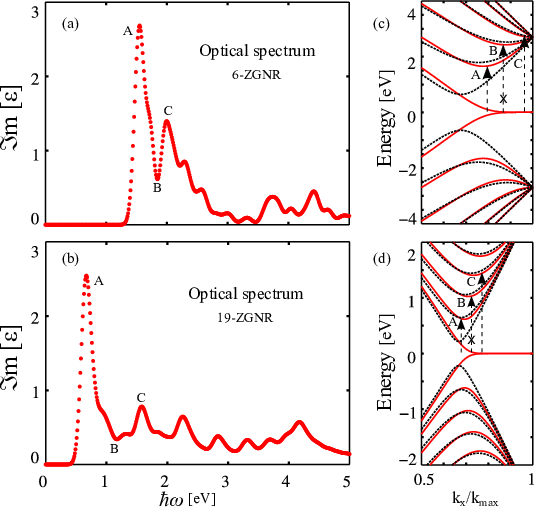
To demonstrate the applicability of our models the imaginary part of the dielectric function ε_i (Eq. 3.4) is calculated numerically for 6-ZGNR and 19-ZGNR (see Fig. 4.8(a) and Fig. 4.8(b)). Peaks in ε_i(ω) indicate absorptions of photons with energy ℏω. From the electronic band-structure in Fig. 4.8(c) it can be found that the peaks in ε_i(ω) are related to transitions from n = 6 to n = 8 (A), and n = 6 to n = 10 (C). The minimum designated as (B) is related to the transition from n = 6 to n = 9 which is forbidden according to the obtained transition rules. The same analysis exists for 19-ZGNR, see Fig. 4.8(b) and Fig. 4.8(d). Therefore, the allowed transitions are from odd to odd and even to even subband numbers, which is in agreement with our analytical derivation.