



Next: 4.3.5 Mesh Refinement at
Up: 4.3 Simulation in FEDOS
Previous: 4.3.3 Assembly of the
4.3.4 Calculation of the Mechanical Stress
The discretization of the mechanical problem presented in Section 4.2.4 yields the linear system of equations
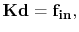 |
(4.96) |
with
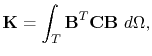 |
(4.97) |
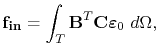 |
(4.98) |
Since
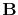 ,
,
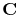 , and
, and
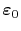 are constant within an element, the assembly of (4.96) is performed in FEDOS using
are constant within an element, the assembly of (4.96) is performed in FEDOS using
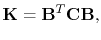 |
(4.99) |
and
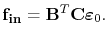 |
(4.100) |
The mechanical problem has to be solved each time step after the solution of the vacancy dynamics problem, as shown in Figure 4.3.
Thus, for the time step 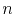 , the internal force vector is determined by the electromigration induced strain given in (3.82), so that
, the internal force vector is determined by the electromigration induced strain given in (3.82), so that
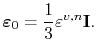 |
(4.101) |
From (3.78), the trace of the electromigration strain for each node of the tetrahedron is calculated by
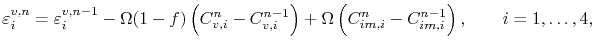 |
(4.102) |
resulting in the element strain which is set in (4.101),
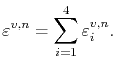 |
(4.103) |
The solution of (4.96) yields the interconnect line deformation due to electromigration.
Once the displacement field
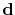 is determined, the electromigration induced stress vector for an element is obtained using (4.60),
is determined, the electromigration induced stress vector for an element is obtained using (4.60),
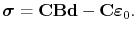 |
(4.104) |
The mechanical stress at each node is obtained by an extrapolation from the stress calculated for the elements, given by (4.104). The stress at a particular node is calculated by performing a weighted average of the stress on all elements connected to the node. Considering a node
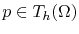 and defining the set of all elements which contain the node as
and defining the set of all elements which contain the node as 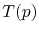 , the mechanical stress at the node
, the mechanical stress at the node 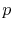 is given by
is given by
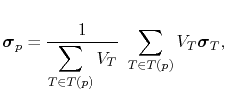 |
(4.105) |
where 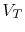 is the volume, and
is the volume, and
 is the stress calculated by (4.104) for the element
is the stress calculated by (4.104) for the element 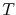 .
.




Next: 4.3.5 Mesh Refinement at
Up: 4.3 Simulation in FEDOS
Previous: 4.3.3 Assembly of the
R. L. de Orio: Electromigration Modeling and Simulation
![]() , the internal force vector is determined by the electromigration induced strain given in (3.82), so that
, the internal force vector is determined by the electromigration induced strain given in (3.82), so that
![]() is determined, the electromigration induced stress vector for an element is obtained using (4.60),
is determined, the electromigration induced stress vector for an element is obtained using (4.60),