2 Overview of Solid Mechanics and the Finite Element Method

Chapter 2
Overview of Solid Mechanics and the Finite Element Method

Microelectronic devices are complex systems fabricated through the manipulation and integration of many different materials. In order to be able to understand and improve such technology a multidisciplinary approach is necessary.

As explained in Section 1.4, mechanical problems in microelectronics are critical issues which may occur during the manufacturing processes or during device operation. In order to improve the devices’ lifetime, a deep investigation into potential mechanical issues is essential. In this chapter the fundamental concepts of the solid mechanics theory needed for the analysis of mechanical problems in microelectronics are described.

The finite element method originated from the needs to solve mechanically related problems. In this work a FEM tool is used to calculate the resulting stress/strain in microelectronic components under several loading conditions and therefore an overview of FEM is presented.

2.1 Continuum Mechanics

The continuum mechanics approach ignores the discrete nature of matter, considering materials as uniformly and continuously distributed throughout regions of space. This simplification leads to the definition of material properties such as conductivity, permittivity, yield strength, coefficient of thermal expansion and simulation quantities such as density, displacement, velocity, etc., as continuous functions of position.

Two main types of equations are used in continuum mechanics [35]:

General equations applicable equally to all materials and referring to universal physical laws.
Equations which describe the mechanical behavior of particular materials know as constitutive equations.

In this section the kinematic and the stress equations are described. Subsequently, a brief description of the constitutive equations concerning elasticity is provided.

2.1.1 Deformation and Strain

This section, which is based on [35, 36], deals with the kinematic relations of a continuous medium. To define the basic deformation and strain concepts we must analyze material kinematics, which refers to the mathematics of motion without considering the masses of objects or the forces which may have caused the motion. Therefore, a kinematic analysis permits to study motion and displacement within a material, without regard to the associated stresses. This permits to analyze the system essentially as a geometric problem. Kinematics is widely applied to solve mechanical problems [36].

In order to describe the motion of a body the definition of a reference coordinate system is necessary (cf. Figure 2.1). At time t = 0 the body B is unloaded and undeformed. The particle of the body can be identified at all times by the set of coordinates X_i where i = 1,2,3 refer to fixed Cartesian axes.

Figure 2.1: Coordinate system. At the reference configuration t = 0 the body B is underformed. The body b is deformed at time t > 0. X₁,X₂ and X₃ refer to the material coordinates at t = 0. x₁,x₂ and x₃ are spatial coordinates at t > 0. u indicates the displacement vector.

At time t > 0 the body may have changed its position and shape (we refer to it as b) and its new position is defined by specifying the position x_i of the particle with previous coordinate X_i in the form

xi = xi(Xp,t), i,p ∈ {1,2,3}

(2.1)

which corresponds to

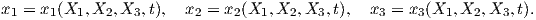x1 = x1(X1,X2, X3, t), x2 = x2(X1, X2,X3, t), x3 = x3(X1, X2,X3, t).

(2.2)

In this equation x_i is the occupied coordinate by the body-point X₁,X₂,X₃ at time t. (2.1) is assumed differentiable with respect to X₁,X₂,X₃ and t.

The deformation of the body can be described by only considering two configurations of the body, an initial and a final configuration where the motion of the body can be regarded as a single-parameter sequence of deformations. In (2.1) the mapping has the unique inverse

X = X (x ,t), i,p ∈ {1,2,3} i i p

(2.3)

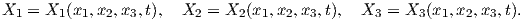X1 = X1 (x1,x2,x3,t), X2 = X2(x1,x2,x3,t), X3 = X3 (x1,x2,x3,t).

(2.4)

From (2.3) the existence of the Jacobian determinant is ensured

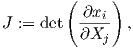( ) ∂xi- J := det ∂Xj ,

(2.5)

which is positive for all points (J > 0). The significance of (2.5) is that the material of the body cannot penetrate itself and that a material occupying a finite non-zero volume V at time t = 0 cannot be compressed to a point or expanded to infinite volume during its motion (dV = JdV ₀).

The coordinates X₁,X₂, and X₃ are known as Lagrangian (or material) coordinates and they refer to distinct material particles at the reference configuration. On the other hand, the coordinates x₁,x₂, and x₃ are known as Eulerian (or spatial) coordinates and they refer to distinct points of space at the deformed configuration. In continuum mechanics both sets of coordinates can be used.

Lagrangian or Eulerian coordinates can be applied to describe the displacement vector u=x-X of a typical particle from its position X, in the reference configuration, to its position x at time t. Using (2.1) as a reference, the displacement vector can be described by

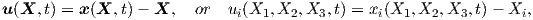u (X, t) = x(X, t)- X, or ui(X1, X2,X3, t) = xi(X1,X2, X3, t) - Xi,

(2.6)

or by using (2.3) as a reference

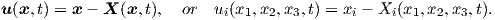u(x,t) = x- X (x, t), or ui(x1,x2,x3,t) = xi - Xi(x1,x2,x3,t).

(2.7)

The material displacement gradient is obtained by a partial differentiation of the displacement vector (2.6) with respect to the Lagrangian coordinate

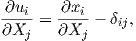∂ui ∂xi ∂X-- = ∂X-- - δij, j j

(2.8)

where δ_ij represents the Kronecker symbol. The spatial displacement gradient is determined by partial differentiation of the displacement vector (2.7) with respect to the Eulerian coordinate

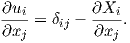∂ui-= δij - ∂Xi-. ∂xj ∂xj

(2.9)

In a similar way the material deformation gradient is defined by

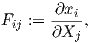F := -∂xi, ij ∂Xj

(2.10)

and the spatial deformation gradient is defined by

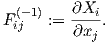(-1) ∂Xi- Fij := ∂xj .

(2.11)

From (2.1) and (2.10) the distance differential dx_i (cf. Figure 2.1) can be expressed by

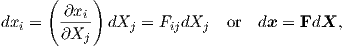( ∂xi ) dxi = ---- dXj = FijdXj or dx = FdX, ∂Xj

(2.12)

where dx is the line element vector and F is the deformation gradient.

F is a second-rank tensor and it can be interpreted as a linear transformation, where the initial element vector dX is mapped onto the corresponding vector dx at time t.

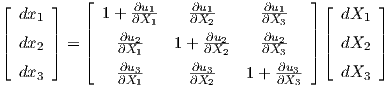⌊ ⌋ ⌊ ∂u ∂u ∂u ⌋ ⌊ ⌋ dx1 | 1+ ∂X11- ∂X12- ∂X13- | dX1 || dx ||= || ∂u2- 1+ ∂u2- ∂u2- || || dX || ⌈ 2 ⌉ ⌈ ∂X1 ∂X2 ∂X3 ⌉ ⌈ 2⌉ dx3 ∂∂uX3- ∂∂uX3- 1+ ∂∂uX3- dX3 1 2 3

(2.13)

An important value is the difference (dx)² - (dX)² for two neighboring particles of a continuum because it can be taken for a suitable measure of strain between the initial and post-displacement configurations. Using (2.10), (2.12), and the summation Einstein’s rule, the measure of strain can be written as

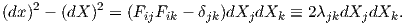2 2 (dx) - (dX ) = (FijFik - δjk)dXjdXk ≡ 2λjkdXjdXk.

(2.14)

In the equation above, the second-order tensor with component λ_ij is known as the Lagrange finite strain tensor:

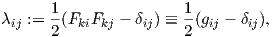1 1 λij := -(FkiFkj - δij) ≡-(gij - δij), 2 2

(2.15)

where the tensor

g = F F ij ki kj

(2.16)

is called right Cauchy-Green tensor.

The Lagrange strain tensor (2.15), described in terms of displacement (2.6), takes the form

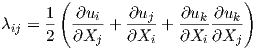( ) 1- -∂ui ∂uj- ∂uk-∂uk- λij = 2 ∂Xj + ∂Xi + ∂Xi ∂Xj

(2.17)

if F_ij from (2.10) and (2.8) is substituted into (2.15).

In addition the strain measure can be formulated by employing the spatial coordinate x_i as a set of independent variables

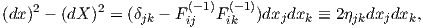(dx)2 - (dX )2 = (δjk - F (-1)F (-1))dxjdxk ≡ 2ηjkdxjdxk, ij ik

(2.18)

where η_jk is the Eulerian finite strain tensor. In terms of displacements (2.7) this tensor takes the form

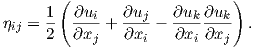( ) 1- ∂ui- ∂uj- ∂uk-∂uk- ηij = 2 ∂xj + ∂xi - ∂xi ∂xj .

(2.19)

If each displacement gradient component ∂u_i∕∂X_j in (2.17) is small compared to δ_ij, the product of the derivatives can be neglected since it is much smaller than the linear term. Therefore, the Lagrange infinitesimal strain tensor is obtained:

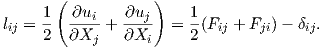( ) 1 ∂ui ∂uj 1 lij = 2- ∂X--+ ∂X-- = 2(Fij + Fji)- δij. j i

(2.20)

Implementing the same methodology for ∂u_i∕∂x_j « δ_ij in (2.19) the Eulerian infinitesimal strain tensor is derived

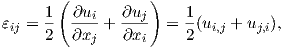( ) ε = 1- ∂ui-+ ∂uj- = 1(u + u ), ij 2 ∂xj ∂xi 2 i,j j,i

(2.21)

which is know as the classical strain tensor.

The Eulerian infinitesimal strain tensor is an approximation which is only valid for small changes and can be expressed as [37]

⌊ ( ) ( ) ⌋ | ∂∂ux11 12 ∂∂u1x2-+ ∂∂ux21 12 ∂∂ux13 + ∂∂ux31 | || 1 (∂u2 ∂u1) ∂u2- 1 (∂u2 ∂u3) || ε = |⌈ 2 (∂x1 + ∂x2) ( ∂x2 ) 2 ∂x3 + ∂y |⌉, 1 ∂u3+ ∂u1 1 ∂u3-+ ∂u2 ∂u3 2 ∂x1 ∂x3 2 ∂x2 ∂x3 ∂x3

(2.22)

or using the engineering notation

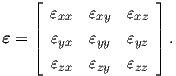⌊ εxx εxy εxz ⌋ || || ε = ⌈ εyx εyy εyz ⌉ . εzx εzy εzz

(2.23)

The components ε_xx, ε_yy, and ε_zz refer to the normal strain and ε_xy=ε_yx , ε_yz =ε_zy , and ε_zx=ε_xz are the shear strain components. In some literature [37], also the following notation is used:

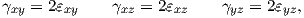γ = 2 ε γ = 2ε γ = 2ε , xy xy xz xz yz yz

(2.24)

however we will stick to the notation from (2.23) in this work. The formulation in (2.21) forms a system of six equations for the three displacement components. The strain components must satisfy the compatibility conditions. Because the displacement field u₁,u₂ and u₃ in any system has to be unique, the strain components are not independent of each other [36]. By eliminating the displacements from (2.21), the compatibility conditions become:

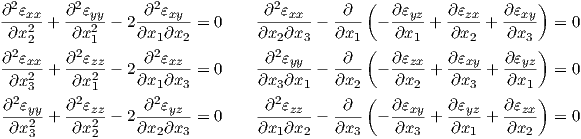( ) ∂2-εxx- ∂2-εyy -∂2εxy- -∂2εxx- -∂-- ∂εyz ∂εzx- ∂εxy- ∂x2 + ∂x2 - 2∂x1 ∂x2 = 0 ∂x2 ∂x3 - ∂x1 - ∂x1 + ∂x2 + ∂x3 = 0 2 2 2 1 2 2 ( ) ∂--εxx-+ ∂-εzz-- 2-∂-εxz- = 0 -∂-εyy- - -∂-- - ∂εzx-+ ∂-εxy-+ ∂-εyz = 0 ∂x23 ∂x21 ∂x1 ∂x3 ∂x3 ∂x1 ∂x2 ∂x2 ∂x3 ∂x1 ∂2εyy ∂2εzz ∂2εyz ∂2 εzz ∂ ( ∂εxy ∂ εyz ∂ εzx ) ∂x2--+ ∂x2--- 2∂x--∂x- = 0 ∂x--∂x- - ∂x-- - -∂x--+ -∂x- + -∂x-- = 0 3 2 2 3 1 2 3 3 1 2

(2.25)

2.1.2 Stress

When a body is deformed internal forces known as stress arise inside it. The stress generates to restore the undeformed state of the body. At mechanical equilibrium the sum of all acting and internal forces must equal to zero. This section, based on [35, 38], provides the relationships between force and stress.

In order to study how the body exterior interacts with the body interior we imagine a closed surface S within a loaded body Z (Figure 2.2).

Figure 2.2: Schematic representation of a body subjected to a force ΔF.

We consider a unit vector n normal to S with direction outward from the interior of S and a small surface element of area ΔS. Two sides of ΔS according to the direction of n are distinguished. The part of material Z lying on the positive side of the normal exerts a force ΔF on the other part that is situated on the negative side of the normal. ΔF is a function of the area and the orientation of surface S. By assuming that ΔF/ΔS approaches a definite limit as ΔS approaches zero the stress vector t (also referred to as the traction vector) can be defined by

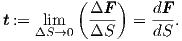( ) ΔF-- dF- t := ΔlSim→0 ΔS = dS .

(2.26)

The components of the stress vector are normal stress and shear stress. Normal stress is defined as 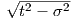σ = t⋅n and shear stress as τ = √ -------
t2 - σ2 .

By considering three specific sections corresponding to the coordinate system x₁, x₂, and x₃ (or x, y, and z) three stress vectors are assigned t1, t2, and t3. The Cartesian components of the stress vectors are denoted by σ_ij, where the index i correlates to the coordinate direction. If we consider the stress vector t1, it can be expressed by:

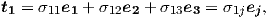t1 = σ11e1 + σ12e2 + σ13e3 = σ1jej,

(2.27)

where e1, e2, and e3 are the unit vectors in the coordinate directions. Similarly the stress vectors t2 and t3 can also be calculated, leading to the general expression

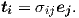ti = σijej.

(2.28)

The stress component σ_ij contains the magnitude, the direction normal to the reference plane (first subscript) and the direction of action (second subscript). The sign of the stress components can be positive or negative.

The stress components σ_ij are usually described by using the engineering notation with a cube, as shown in Figure 2.3. The stress components act perpendicular (normal stress) and parallel (shear stress) to the faces of the cube. Normal stresses can pull the cube (tensile normal stress) or push it (compressive normal stress).

The stress tensor (also called Cauchy stress tensor) σ is a second order tensor which consists of normal and shear components acting on an infinitesimal element.

Figure 2.3: Stress components on an infinitesimal cube.

Considering a 3D system, the stress tensor is described through nine stress components [39]

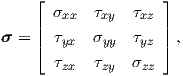⌊ ⌋ σxx τxy τxz σ = || τyx σyy τyz ||, ⌈ ⌉ τzx τzy σzz

(2.29)

where σ_xx, σ_yy, and σ_zz are the normal stresses and τ_xy, τ_yx, τ_yz, τ_zy, τ_zx, and τ_xz are the shear stress components.

If the stress tensor is symmetric the number of stress components reduces to six because

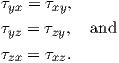τyx = τxy, τ = τ , and yz zy τzx = τxz.

(2.30)

By applying Newton’s first law to a solid subjected to body force components represented by F_x, F_y, and F_z, the equilibrium conditions of the stress components can be derived [35, 36, 37]. F_i could be alternatively described as F_i = ρb_i, where ρ is the density of the body and b_i is the force per unit of mass. An equilibrium of an arbitrary volume V of a continuum requires that the resulting moment and force acting on the volume be zero; therefore, the sum of surface and body forces satisfy an integral relation

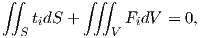∫∫ ∫ ∫∫ tidS + FidV = 0, S V

(2.31)

where F_i represents the component of body force and t_i is the stress component acting on an arbitrarily oriented infinitesimal area ndS (t_i = σ_ijn_j). By converting the resulting surface integral to a volume integral using the Gauss’s divergence theorem, we obtain

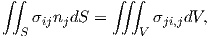∫∫ ∫ ∫∫ σijnjdS = σji,jdV, S V

(2.32)

and then equation (2.31) becomes

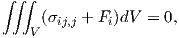∫∫∫ (σij,j + Fi)dV = 0, V

(2.33)

where σ_ij,j ≡ ∂σ_ij∕∂x_j is the divergence of the stress tensor. Because the volume in (2.33) is arbitrary the integral vanishes and we obtain the equilibrium conditions:

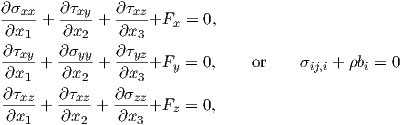∂σxx- ∂τxy ∂τxz ∂x1 + ∂x2 + ∂x3 +Fx = 0, ∂τ ∂σ ∂τ --xy + --yy-+ --yz+Fy = 0, or σij,i + ρbi = 0 ∂x1 ∂x2 ∂x3 ∂τxz + ∂τxz+ ∂σzz+F = 0, ∂x1 ∂x2 ∂x3 z

(2.34)

The Cauchy stress tensor σ is used to model small deformations (infinitesimal strain theory) and it is a fundamental concept in the theory of linear elasticity. For large deformations the concept of the Piola-Kirchhooff stress tensor is used [36].

In engineering the concept of the scalar Von Mises effective Stress is commonly used to predict yielding of materials under a loading conditions as well as other physical phenomena [36]

------------------------------------------ ∘ 1 σmises = 2 [(σxx - σyy)2 + (σxx - σzz)2 + (σyy - σzz)2].

(2.35)

2.1.3 Constitutive Laws

The equations described above are applicable for all continuous materials. However additional equations, called constitutive equations, are necessary to describe the mechanical behavior of any particular material.

Four theories for material behavior can be distinguished [35]:

Elasticity: Material deformation is reversible and it returns to its original shape and size once loads are removed. For most materials the stress is a linear function of the strain. The strain depends only on the applied stress and does not depend on the history of loading.
Plasticity: If the material is under modest stresses it responds elastically. If the stress exceeds a critical magnitude the specimen is permanently changed in size and shape. During this phase the stress is not a linear function of the strain.
Viscoelasticity: Materials combine elastic and viscous behavior. It is characterized by a time-dependent response and by the load or deformation history.
Viscoplasticity: Material deformation depends on the rate of the applied load. Unlike with plasticity the material is under a creep flow which is a function of time and the applied load.

Creep behavior exists in viscoelasticity and viscoplasticity theories. Creep is the phenomenon where a solid material moves slowly or deforms permanently under stresses.

Materials are additionally described as brittle or ductile [37]. In brittle materials rupture occurs without any noticeable prior deformation, behaving elastically before rupture. For ductile material the rupture arrives after a plastic deformation.

Figure 2.4: Example of stress-strain curve for a ductile material.

The different material behaviors listed above can be analyzed using stress-strain curves. For each material a unique relationship between stress and strain can be found. Stress-strain curves are obtained by recording the strain at distinct intervals of applied stress. Figure 2.4 depicts an example of a stress-strain curve with an elastic-plastic behavior for a ductile material. In the plot several characteristic points can be identified: The yield strength point defines the stress where a material starts to plastically deform. Below this value the material behaves elastically. The ultimate strength point defines the maximum stress which a material can withstand during deformation. The fracture strength point represents the stress where the specimen fails or fractures. Usually, in brittle materials the stress-strain curve is only valid until the yield strength is reached, at which point fracture occurs. The yield strength in brittle materials is refereed to as the fracture strength.

The stress-strain curve describes the elastic modulus E (also known as Young’s modulus). E is a typical mechanical property which defines a reversible, time-independent elastic strain induced by a load. It is calculated by dividing the tensile stress by the strain of the elastic part of the stress-strain curves. On the other hand, ductility is a mechanical property for plastic material and it defines the maximum strain which the material can withstand without breaking.

The behavior of materials and their properties are correlated to the arrangement of atoms in the material body. Single-crystal is a body where atoms are ordered in a pattern which repeats itself; therefore, only a single crystalline phase is present. Polycrystalline materials are composed of more than one crystal (grains) and often combine different crystalline phases (cf. Figure 2.5).

Figure 2.5: Polycrystalline material.

At the atomic scale elastic and plastic deformations are significantly different (cf. Figure 2.6) [40]. Elastic deformation results in each atom moving under a load. On the other hand, in plastic deformation, only a few atoms move and the phenomenon is anisotropic (even though it is usually considered as an isotropic phenomenon in polycrystalline materials). Plasticity is the phenomenon which moves atoms through many interatomic distances relative to their positions. During plastic deformation the material tends to preserve the crystal structure, therefore this limits the way in which the plastic deformation can appear. A typical deformation is represented by a slip system containing a particular slip plane in a given slip direction. Slip planes are crystallographic planes with the highest density of atoms. The slip direction and the magnitude of a dislocation in the slip plane are defined by the Burgers vector [41, 42]. Each material has a characteristic slip system, in which dislocations are carriers of plastic deformation [40]. Dislocations are one-dimensional lattice defects where atoms are out of position in the crystal. They move and are generated under the action of high shear stresses because the atoms in the vicinity of the dislocation line rearrange their bonds. During this process the work done is dissipated through lattice vibration, and the dislocation movement results in a relative slip.

Figure 2.6: Atom movements in elastic and slip deformation.

It is therefore clear that the plastic mechanism is influenced by the microstructural features such as slip plane, lattice imperfections, alloying, and impurity elements. The plasticity is also influenced by the movement, multiplication, and interaction between dislocations [43]. Therefore, the microstructures of materials define properties such as elasticity, plasticity, and creep.

An elastic-plastic material is usually studied assuming that the strains ε and strain increments dε consist of an elastic and a plastic component [37]:

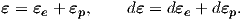ε = εe + εp, dε = dεe + dεp.

(2.36)

We take a closer look on the elastic component of a linear stress-strain relationship in the next subsection. For the plastic component a different constitutive law, based on plastic strain increments or total plastic strains, are in use [35, 37].

2.1.3.1 Elasticity

For a linear elastic material, assuming small (infinitesimal) strain (∂u_i∕∂x_j « 1), stresses and strains are related [36, 37, 44] through the following constitutive equation:

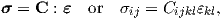σ = C : ε or σij = Cijklεkl,

(2.37)

where C indicates the elasticity tensor. The equation above is known as Hooke’s law and the two dots indicates a summation over two index pairs. C is a fourth-order tensor with 81 components C_ijkl. Since the stress and strain tensors are symmetric it follows that

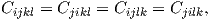Cijkl = Cjikl = Cijlk = Cjilk,

(2.38)

which reduces the number of independent components from 81 to 36. Equation (2.37) can be inverted and the elasticity law becomes

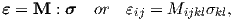ε = M : σ or εij = Mijklσkl,

(2.39)

where M is the compliance tensor. The components M_ijkl have the same symmetry properties as C_ijkl.

For an isotropic material, C is an isotropic tensor which is described by only two independent constant:

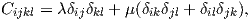C = λδijδ + μ(δ δ + δ δ ), ijkl kl ik jl il jk

(2.40)

where λ and μ are the Lame´constants defined as

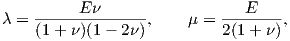λ = -----E-ν------, μ = ---E----, (1+ ν)(1- 2ν) 2(1 + ν)

(2.41)

where E is the Young’s modulus, ν is the Poisson’s ratio, and μ is the shear modulus. Substituting (2.40) in (2.37), an isotropic material is described as

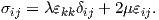σij = λεkkδij + 2μεij.

(2.42)

2.2 Plane Strain and Plane Stress

Many 3D solid mechanics problems can be treated as 2D problems. Plane strain and plane stress are two idealized stress configurations, which simplify problem analysis [37]. The two approximations are described by using the following engineering notation with coordinates x, y, z, displacements u_x, u_y, u_z, strains ε_xx, τ_xy, … and stresses σ_xx, τ_xy, ….

2.2.1 Plane Strain

The plane strain is defined to be a state which assumes that u_z, ε_zz, γ_xz, γ_yz, τ_xz, and τ_yz are equal to zero. Plane strain can be idealized as long wire where stress components act perpendicular to its length. Therefore, the equilibrium conditions reduce to

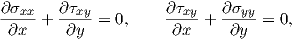∂ σxx ∂τxy ∂τxy ∂σyy -∂x--+ ∂y--= 0, -∂x- + -∂y--= 0,

(2.43)

the kinematic relations to

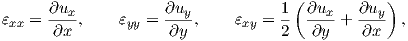∂ux ∂uy 1 (∂ux ∂uy) εxx = -∂x-, εyy = ∂y-, εxy = 2- -∂y- + ∂x-- ,

(2.44)

and compatibility conditions become

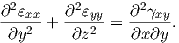∂2εxx ∂2εyy ∂2γxy ---2-+ ---2-= -----. ∂y ∂z ∂x∂y

(2.45)

This assumption permits to reduce the stress-strain relation to

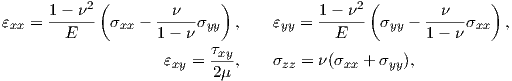1- ν2 ( ν ) 1 - ν2 ( ν ) εxx = ------ σxx - -----σyy , εyy = ------ σyy - -----σxx , E 1 - ν τ E 1- ν εxy = -xy, σzz = ν(σxx + σyy), 2μ

(2.46)

where μ is the shear modulus.

2.2.2 Plane Stress

On the other hand, in the plane stress approximation, σ_zz, τ_xz, τ_yz, γ_xz, and γ_yz are zero and the other stress and strain components are independent of z. Here, the problem can be simplified to a 2D thin plate problem where the stress components act along the plane. By applying the plane stress assumption to the equilibrium conditions, kinematic relations, and compatibility conditions as shown in (2.43)-(2.45) the stress-strain relation reduces to

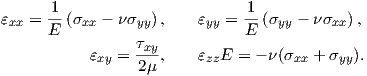ε = 1-(σ - ν σ ), ε = -1(σ - νσ ), xx E xx yy yy E yy xx ε = τxy-, ε E = - ν(σ + σ ). xy 2μ zz xx yy

(2.47)

2.3 Source of Residual Stress in Thin Films

In microelectronic devices, thin films can have residual stresses, which arise due to two main sources: intrinsic and thermal stress [45]. High values of residual stress can affect the quality and performance of thin films and subsequently of the entire devices. Therefore, the investigation of the origin of the residual stress is a fundamental aspect to examine.

2.3.1 Intrinsic Stress

Intrinsic stress emerges during the deposition processes (e.g. sputtering, spraying, painting, spin coating, CVD, PVD, and electrodeposition). The magnitude of the intrinsic stress depends on the process, deposition temperature, and deposited material. During the deposition process, the microstructure evolves from single atom islands to a uniform film, influencing the magnitude of intrinsic stress [45]. In Chapter 5 a detailed description of intrinsic stresses in thin films is reported.

2.3.2 Thermal Strain and Thermal Stress

In absence of mechanical loads a body can deform due to temperature changes. This deformation is called thermal deformation, which gives rise to so called thermal strain inside the body [39]. For small temperature changes the thermal strain is linearly proportional to the temperature change and it is described by the Coefficient of Thermal Expansion (CTE). CTE is a material property which describes how a material expands upon heating or contracts upon cooling. For changes in volume the volumetric CTE can be expressed as

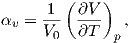1 ( ∂V ) αv = --- --- , V0 ∂T p

(2.48)

where V ₀ is the initial volume, and p indicates a pressure constant. For changes in length, α_v is denoted as α_l, but instead of a change in volume V is substituted by length l

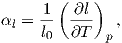( ) 1- ∂l- αl = l0 ∂T p,

(2.49)

where l₀ indicates the initial length. For an isotropic material, where α_v = 3α_l the thermal strain can be expressed as

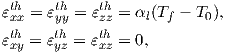εthxx = εtyhy = εthzz = αl(Tf - T0), th th th εxy = εyz = εxz = 0,

(2.50)

where the change from T₀ to T_f corresponds to the temperature variation. The shear components are all zero because the thermal expansion is volumetric.

Thermal stress is the stress generated in a constrained structure due to a thermal expansion or contraction. Two different set of constraints are possible: external constraint and internal constraint. External constraint can be every external object which obstruct the free expansion or contraction of the system, when temperature changes occur. Internal constraint usually appear in composite systems, formed by different materials, or when a nonuniform temperature distribution is present. Due to the different CTEs every material behaves differently under thermal variation. The thermal strain generated in a material can affect and then generate thermal stress, thereby impacting the system.

The relationships between stress and strain for an isotropic material, including the thermal strain are given as

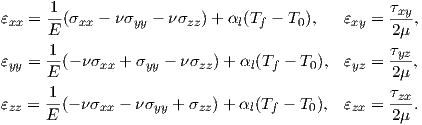1 τxy εxx = E-(σxx - νσyy - νσzz) + αl(Tf - T0), εxy = 2μ-, εyy = 1-(- ν σxx + σyy - νσzz)+ αl(Tf - T0), εyz = τyz, E 2μ ε = 1-(- ν σ - νσ + σ )+ α (T - T ), ε = τzx. zz E xx yy zz l f 0 zx 2μ

(2.51)

2.4 Virtual Work

The principle of virtual work is applied to study the mechanics of deformable bodies. The term virtual refers to the implementation of infinitesimal displacements, called virtual displacement, which do not represent a real displacement acting on the system. By considering the equilibrium equations of a system, where all the forces acting on a system in static equilibrium must be equal zero, virtual displacement can be applied and the resulting deformation of the body can be obtained [36, 37].

We consider a body of volume V in equilibrium, where a prescribed traction t on boundary Γ_t and a prescribed displacement u on boundary Γ_u are

σijnj = ti on Γ t, ui = 0 on Γ u.

(2.52)

To derive the concept of the virtual work it is necessary to recall the equilibrium condition and the classic strain tensor:

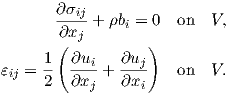∂-σij + ρbi = 0 on V, (∂xj ) 1 ∂ui ∂uj εij = -- ----+ ---- on V. 2 ∂xj ∂xi

(2.53)

δu is defined as virtual displacement and it has to satisfy the boundary condition on Γ_u. By employing δu a virtual strain is defined

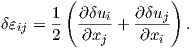( ) 1 ∂ δui ∂ δuj δεij = -- -----+ ----- . 2 ∂xj ∂xi

(2.54)

The equilibrium condition is multiplied by the virtual displacement

( ∂σ ) ---ij + ρbi δui = 0. ∂xj

(2.55)

By using the product rule

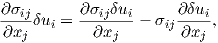∂σij ∂σijδui ∂δui ----δui = -------- σij-----, ∂xj ∂xj ∂xj

(2.56)

and the symmetry of (2.54) equation (2.55) can be rewritten as

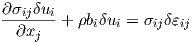∂σijδui+ ρb δu = σ δε ∂xj i i ij ij

(2.57)

which, when is integrated over the volume of V becomes

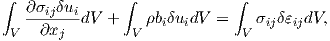∫ ∫ ∫ ∂σijδui V ∂xj dV + V ρbiδuidV = V σijδεijdV,

(2.58)

Gauss’s divergence theorem is applied at the first volume integral, becoming a surface integral

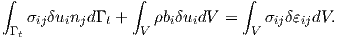∫ ∫ ∫ σijδuinjdΓ t + ρbiδuidV = σijδεijdV. Γ t V V

(2.59)

By using the boundary condition the equation above can be rewritten in a simplified form

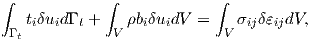∫ ∫ ∫ Γ t tiδuidΓ t + V ρbiδuidV = V σijδεijdV,

(2.60)

where the integrals on the left represent the virtual work done by external forces. On the right hand side the integral represents the virtual work done by internal forces. The system is in equilibrium if the entire virtual work of the imposed virtual displacements vanishes, therefore (2.60) is equivalent to (2.34).

2.5 Fracture Mechanics

Fracture is a degradation process which leads to the generation of new surfaces. Fracture develops through cracking, which is the development of displacement discontinuity surfaces within the solid. Previously a continuum-mechanical analysis was presented, however a microscopic approach is necessary to understand the role of the microstructure in fracture mechanics [37]. At the microscopic level, the fracture process consists of breaking the bonds between elements (atoms, ions, molecules, etc.). The bonding force between two elements is described by

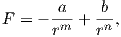F = --am- + -bn, r r

(2.61)

where a, b, m, and n are constants which characterize the bond type and r is the distance between elements. The first term is the attractive force, while the second term describes a repulsive force. During the separation of elements (fracture) a negative material-specific work W^B is performed by the bonding force. This work is the surface energy necessary to form new surfaces in the immediate neighborhood, leading to an instant change of the lattice geometry. From the macroscopic point of view, considering the material as a continuum and neglecting dissipative processes (heat), the work of bonding forces is converted into the surface energy of the body

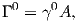Γ 0 = γ0A,

(2.62)

where A is the newly created surface and γ⁰ is the surface energy density.

In a polycrystalline material the separation of atomic planes (microcracks) is often combined with pronounced microplastic processes (dislocations). The dislocation pile-up at obstacles is an important phenomenon during microcrack formation.

It can cause a high stress concentrations leading to bond breaking along favored lattices places:

Transcrystalline cleavage occurs when a crack runs through several grains, and the separation surface changes according to local lattice planes.
Intercrystalline fracture separation between weak grain boundaries occurs on account of dislocation pile-up or grain boundary sliding takes place along these boundaries.

These processes describe fracture in brittle materials. In plastic deformation the load is not enough to break the atomic bonds but it is large enough to produce permanent deformation by shearing atomic planes (dislocations); therefore, the failure is the plastic regime.

Cracks are classified from different phenomenological viewpoints. A stationary crack is a crack which does not change in length. If the crack starts to propagate and it becomes non-stationary a specified load or deformation is called crack initiation. Crack propagation can further be distinguished as stable, when the increase in crack length requires an increases external load, or unstable, when the crack advances without any increase in the external load. In Chapter 4 the basis of fracture mechanics are described in further details.

2.6 FEM

In Section 1.5 the basic ideas behind the finite element method are described. In this section some mathematical concepts of FEM are presented [46, 47, 48]. The solution to a problem is obtained by applying a variational method. The weighted residual method and its different approaches are initially described. Subsequently the so called weak formulation is reported. These methods permit to calculate an approximate solution in the form of a linear system by minimizing an associated error function. A description of the spatial discretization is also presented in this section. At the end of the chapter FEM is applied to solve a mechanical problem.

A physical problem can often be described by the following general differential equation

[ ] d-- du(x)- du(x)- dx a(x) dx + b(x ) dx + c(x)u(x) - f(x) = 0,

(2.63)

where u(x) is the unknown function. The coefficient functions a(x), b(x), and c(x) and the source term f(x) describes a physical problem. For example, if we consider an elastic bar, we must solve for u(x) where the parameter a corresponds to the bar stiffness E ⋅ A (E is the Young’s modulus and A the cross sectional area) and f is the applied body load.

For a well-defined problem set, boundary conditions are required. There are three types of boundary conditions: The first is called Dirichlet boundary condition where a domain Ω has a boundary along which the displacement is a constant, defined by

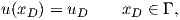u (xD ) = uD xD ∈ Γ ,

(2.64)

where Γ represents the boundary. The second kind is called the Neumann boundary condition where the slope of the boundary value is known

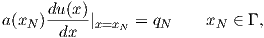du(x)- a(xN ) dx |x=xN = qN xN ∈ Γ ,

(2.65)

where q_N represents a scalar function. The third kind is called the Robin boundary condition

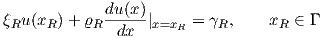du (x ) ξRu(xR) + ϱR--dx--|x=xR = γR, xR ∈ Γ

(2.66)

where ξ_R, ϱ_R, and γ_R are parameters given by the physical problem. This condition represents a weighted sum of the value and the slope of the function at the boundary.

2.6.1 Weighted Residual Method

In this section we describe the general method of the weighted residual and the derivation of the solution using different approaches.

One-dimensional physical problems in a domain Ω can often be described by the differential equation (2.63); however, to describe mathematical concepts of FEM it is more useful represent a differential equation with the linear operator L{…}

[ ] 0 d du0(x) du0(x) 0 L {u (x)} = dx- a(x)--dx-- + b(x)--dx--+ c(x)u (x) = f(x).

(2.67)

In (2.67) u⁰(x) represents the exact or real solution of the problem subject to boundary conditions along the boundary Γ and to the prescribed geometry. The solution u⁰(x) solves the differential equation along every point of the domain x ∈ Ω. To simplify the mathematical equation, in the following derivations we indicate

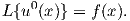L{u0(x)} = f(x).

(2.68)

When an exact analytical solution cannot be found, an approximated solution of the problem is obtained by employing numerical methods. The goal is to calculate a useful approximation of the exact solution

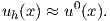uh(x) ≈ u0(x).

(2.69)

In the case of the weighted residual method [47, 49] an approximation of the solution of the following form is chosen

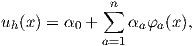∑n uh(x) = α0 + αa φa(x), a=1

(2.70)

where α₀ has to satisfy the non-homogeneous boundary conditions, φ_a(x) are a set of linear independent basis functions, and α_a are the free parameters of the approximation approach. If the solution has to satisfy homogeneous boundary conditions the variable α₀ can be omitted.

A local error know as residual r is obtained by inserting the approximation function for u⁰(x) into the differential equation (2.67)

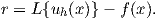r = L{uh(x)} - f(x).

(2.71)

Performing an integration over the entire domain Ω the residual r, weighted with a weighting function W(x), gives

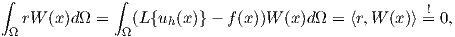∫ ∫ ! Ω rW (x)dΩ = Ω (L {uh(x)}- f(x))W (x )d Ω = ⟨r,W (x)⟩= 0,

(2.72)

which represents an inner product. By choosing the appropriate α_a parameters of the approximated solution, the average r can be forced r to zero over the entire domain.

W(x) is referred to as the test function and it allows for an arbitrary weighting of the error in the domain Ω. Usually, the structure of the test function is defined as the approximation function u_h(x) by a sum of a weighted basis function set:

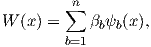∑n W (x ) = βbψb(x), b=1

(2.73)

where β_b are arbitrary coefficients and ψ_b(x) are linear independent shape functions. The choice of the shape functions ψ_b(x) depends on the applied method:

The Point-Collocation Method is based on the Dirac delta function. The error r vanishes at the n selected points x₁, x₂,..,x_n ∈ Ω. At those so called collocation points the approximated solutions satisfies the differential equation. Thereby, the test function is set as:
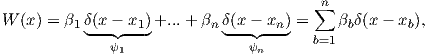$∑n W (x) = β1δ(x - x1)+...+ βn δ(x- xn )= βbδ(x - xb), ◟---◝◜--◞ ◟--◝◜---◞ b=1 ψ1 ψn$ (2.74)

where the Dirac delta function is:

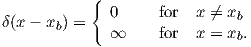${ 0 for x ⁄= x δ(x- xb) = b ∞ for x = xb.$ (2.75)

By applying the test function (2.74) in the inner product (2.72) and considering the property of the Dirac delta function,

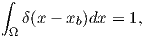$∫ δ(x - x )dx = 1, Ω b$ (2.76)

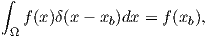$∫ Ω f(x)δ(x - xb)dx = f(xb),$ (2.77)

and choosing β_b = δ_ib for i ∈{1,…,n}, this results in a system of n linear independent equations. The property of the delta function leads to ∫ _ΩrW(x)dΩ = r = 0, therefore no integral needs to be calculated within the point-collocation procedure. The parameters α_a can be calculated by solving the system:

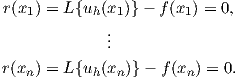$r(x1) = L{uh(x1)} - f(x1) = 0, ... r(xn) = L{uh(xn)} - f(xn) = 0.$ (2.78)

Because L{…} is linear in this argument these equations can be further derived

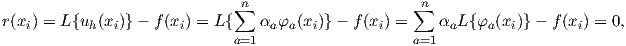$∑n ∑n r(xi) = L{uh (xi)} - f(xi) = L { αaφa (xi)} - f(xi) = αaL {φa(xi)}- f(xi) = 0, a=1 a=1$ (2.79)

which can be written in matrix form

$(L{φa (xi)})i,a(αa)a - (f(xi))i = 0 or L α = f i,a ∈ {1,...,n}.$ (2.80)

The results can be obtained by inverting the matrix:

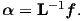$-1 α = L f.$ (2.81)

By obtaining the parameters α_a and by plugging them in (2.70) the approximated solution is derived.
The Subdomain-Collocation Procedure is considered to be a variation of the point collocation method. The domain Ω is divided in non overlapping subdomains Ω_b. The shape functions of the test functions are chosen in such a way that ψ_b(x) = 1 in Ω_b and zero otherwise:
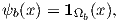$ψb(x ) = 1Ω (x), b$ (2.82)

where the indicator function is defined by

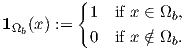${1 if x ∈ Ω , 1 Ωb(x) := b 0 if x ∕∈ Ωb.$ (2.83)

Therefore the test function is defined as

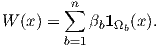$∑n W (x) = βb1Ωb(x). b=1$ (2.84)

The integral of the error becomes zero over the different domains:

$∫ ∑n ∫ ! Ω r(x)W (x)dΩ = βb Ω r(x)dΩb = 0. b=1 b$ (2.85)

β_b are chosen as in the point-collocation procedure (β_b = δ_ib for i ∈{1,…,n}) resulting in the following n-equation system:

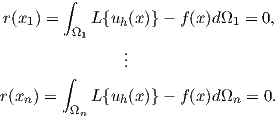$∫ r(x ) = L{u (x)} - f(x)dΩ = 0, 1 Ω1 h 1 . .. ∫ r(xn ) = Ω L{uh(x)} - f(x)dΩn = 0. n$ (2.86)

The parameters α_a can subsequently be calculated as described in the point-collocation method.
The Least Squares Method has a test function defined as
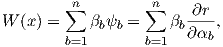$∑n ∑n -∂r- W (x) = βbψb = βb∂α , b=1 b=1 b$ (2.87)

where β_b is chosen as β_b = δ_ib for i ∈{1,…,n}.
In the method of least squares the weighted integral is written as

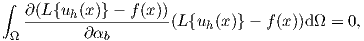$∫ ∂(L-{uh(x)}--f(x))(L {uh(x)}- f(x))dΩ = 0, Ω ∂ αb$ (2.88)

where, employing the chain rule, the following form can be derived:

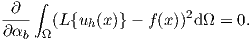$∫ -∂-- (L {u (x)}- f (x))2dΩ = 0. ∂ αb Ω h$ (2.89)

This finally leads to the minimization of the square residual:

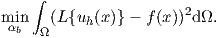$∫ min (L {uh(x)}- f(x))2dΩ. αb Ω$ (2.90)

In detail, the employed test function is

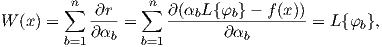$∑n n∑ W (x) = -∂r-= ∂(αbL{-φb}--f-(x-))-= L {φb}, b=1∂αb b=1 ∂αb$ (2.91)

thus this equation can be inserted in (2.88)

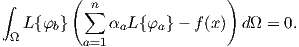$∫ (∑n ) L{φb} αaL{φa }- f (x ) dΩ = 0. Ω a=1$ (2.92)

The equation can then be rewritten as

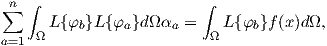$n ∫ ∫ ∑ ΩL {φb}L{φa }dΩαa = ΩL {φb}f(x)dΩ, a=1$ (2.93)

and

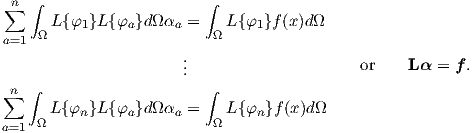$∑n ∫ ∫ L {φ1}L {φa}dΩ αa = L {φ1}f(x)dΩ a=1 Ω Ω .. . or L α = f. ∑n ∫ ∫ L {φn}L {φa}dΩ αa = L {φn}f (x )d Ω a=1 Ω Ω$ (2.94)

From this linear system it is possible to obtain the α_a parameters necessary to describe the approximated function.
The Petrov-Galerkin Procedure is a method where the set of test functions ψ_b(x) and the set of basis functions φ_a(x) are different. The test function is defined as
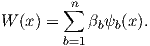$∑n W (x) = βbψb (x ). b=1$ (2.95)

Equation (2.95) can be plugged into (2.72)

$∑n ∑n ∫ βbαa ψb (x )(L{φa} - f(x))dΩ = 0 b=1 a=1 Ω$ (2.96)

The parameters β_b are chosen as β_b = δ_ib for i ∈{1,…,n} and (2.96) is re-written as

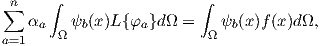$∑n ∫ ∫ αa ψb (x )L {φa}dΩ = ψb(x)f (x )dΩ, a=1 Ω Ω$ (2.97)

which can be written as system of linear equations:

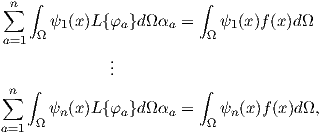$∑n ∫ ∫ ψ1(x)L{φa }dΩαa = ψ1(x)f(x)dΩ a=1 Ω Ω .. . ∑n ∫ ∫ Ω ψn(x)L{φa }dΩαa = Ωψn (x )f (x )d Ω, a=1$ (2.98)

from which is possible to obtain the α_a of the approximated function.
The Galerkin Procedure is a method based on choosing the same set of shape functions for the approximation ψ_b(x) and the weighting φ_a(x) function. Therefore the weighting function for this method is defined by
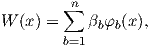$∑n W (x) = βbφb (x ), b=1$ (2.99)

where β_b are the coefficients which can be chosen arbitrary.
The definition (2.99) can be plugged into (2.72), obtaining

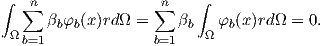$∫ ∫ ∑n ∑n Ω βbφb (x )rdΩ = βb Ω φb(x)rdΩ = 0. b=1 b=1$ (2.100)

By inserting the approximation function (2.70) in the above equation we obtain

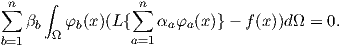$n ∫ n ∑ β φ (x)(L {∑ α φ (x )} - f(x))dΩ = 0. b=1 b Ω b a=1 a a$ (2.101)

This integral can be separated

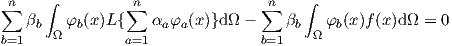$∑n ∫ ∑n ∑n ∫ βb φb(x)L{ αa φa(x)}dΩ - βb φb(x)f(x)dΩ = 0 b=1 Ω a=1 b=1 Ω$ (2.102)

and due to the linearity of the differential operator the summation can be extracted

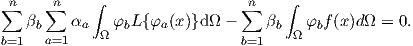$∑n n∑ ∫ ∑n ∫ βb αa φbL {φa(x)}dΩ - βb φbf (x )dΩ = 0. b=1 a=1 Ω b=1 Ω$ (2.103)

The weighting functions can be arbitrary chosen and therefore we consider only one β_b = 1 and the other zero, resulting in

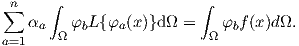$n ∫ ∫ ∑ αa Ω φbL{φa (x)}dΩ = Ω φbf(x)dΩ. a=1$ (2.104)

Using this method for all b results in n equations, which leads to a system of linear equations

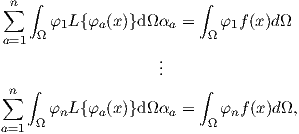$∑n ∫ ∫ φ1L {φa(x)}dΩ αa = φ1f(x)dΩ a=1 Ω Ω ... ∫ ∫ ∑n Ω φnL {φa(x)}dΩ αa = Ω φnf(x)dΩ, a=1$ (2.105)

which can be expressed in matrix form by

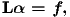$Lα = f,$ (2.106)

with the following definitions:

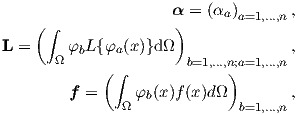$α = (αa)a=1,...,n , (∫ ) L = φbL{φa (x )}d Ω , Ω (∫ b=1,...,n;)a=1,...,n f = φ (x)f(x)dΩ , Ω b b=1,...,n$ (2.107)

where α is the vector of the unknown α_a coefficients, f is the load vector, and L is called stiffness matrix. Many FEM implementations are based on this procedure together with the weak formulation described in the next subsection.

2.6.2 Weak Formulation

A solution to (2.63), which is called the strong formulation, is very difficult or impossible for typical engineering problems. It requires continuity on the dependent field variables and that the approximation function be differentiable up to the order of the differential equations. For such problems, the weak formulation can be used, which mathematically corresponds to the strong formulation. Usually the weak formulation has an integral form and it requires a weaker continuity on the field variables. It also allows for a reduction in the necessity for the differentiability of the approximation function by one order and permits a native incorporation of the Neumann boundary condition [50]. Here the transition from the strong formulation to the weak formulation is described [48].

In a 3D system a differential equation in domain Ω can be defined by:

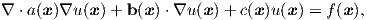∇ ⋅a(x)∇u (x)+ b (x)⋅∇u (x) + c(x )u(x) = f (x ),

(2.108)

where f(x) is the source term. This equation corresponds to the strong formulation. Furthermore the problem must fulfill boundary conditions, which could be given in the following way.

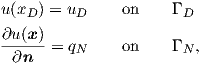u(x ) = u on Γ D D D ∂u-(x-)= qN on Γ N, ∂n

(2.109)

where n is the normal. The union Γ = Γ_D ∪ Γ_N is at the boundary Γ of the domain Ω. On Γ_D the Dirichlet boundary condition and on Γ_N the Neumann boundary condition are implemented. The function u(x) has to be solved on the entire simulation domain Ω.

The weak formulation is obtained by multiplying (2.108) by (2.73) and integrating over the entire domain Ω (cf. inner product)

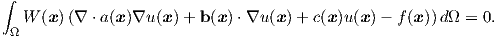∫ W (x )(∇ ⋅a(x)∇u (x)+ b (x )⋅∇u (x)+ c(x )u (x )- f(x))dΩ = 0. Ω

(2.110)

Subsequently, the Green’s first integration theorem is applied

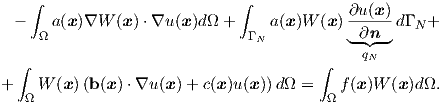∫ ∫ ∂u-(x) - Ωa(x )∇W (x) ⋅∇u (x)dΩ + Γ N a(x)W (x)-∂n--dΓ N+ ◟ ◝q◜N ◞ ∫ ∫ + W (x)(b(x) ⋅∇u (x)+ c(x)u(x))dΩ = f (x )W (x)dΩ. Ω Ω

(2.111)

Therefore, the weak formulation for the initial boundary problem becomes:

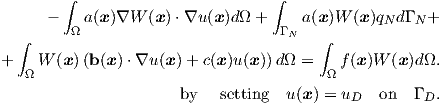∫ ∫ - a(x )∇W (x )⋅∇u (x)dΩ + a(x)W (x)q dΓ + Ω Γ N N N ∫ ∫ + W (x)(b(x) ⋅∇u (x)+ c(x)u(x))dΩ = f (x )W (x)dΩ. Ω Ω by setting u(x) = uD on Γ D.

(2.112)

The Neumann boundary conditions are incorporated in (2.112), while the Dirichlet boundary condition u_D must be explicitly enforced. Equation (2.112) is mathematically equivalent to (2.108) in the case that the solution is sufficiently smooth.

The approximated solution can be obtained by plugging the equations (2.73) and (2.70) into (2.112) and by choosing β_b = δ_ib for i ∈{1,…,n},

[ ] ∑ ∫ ∫ ∫ αa - Ω a(x)∇ φb ⋅∇ φadΩ + Ωφbb(x) ⋅∇φad Ω + Ω c(x )φb φadΩ a ∫ ∫ = - a(x)φbqN dΓ N + f(x)φbdΩ, Γ N Ω

(2.113)

where for b ∈{1,…,n} the solution results in a system of n equations which can be expressed in matrix form by

L α = f

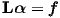(2.114)

whit values

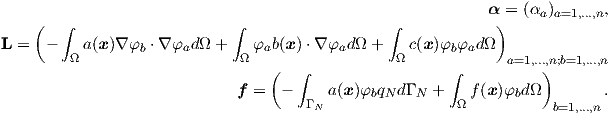α = (αa)a=1,...,n, ( ∫ ∫ ∫ ) L = - a(x)∇φb ⋅∇ φadΩ + φab(x) ⋅∇φad Ω + c(x )φb φadΩ Ω Ω ( ∫ Ω ∫ a=1,...),n;b=1,...,n f = - a(x )φ q dΓ + f(x )φ dΩ . Γ N bN N Ω b b=1,...,n

(2.115)

The α_a parameters for the approximated function can subsequently be obtained.

2.6.3 Spatial Discretization

FEM is based on splitting complex domains or subdomains into geometrically simple shapes called finite elements. These elements, forming a mesh, are defined in 1D by intervals, in 2D usually by triangles or quadrilaterals, and in 3D usually by tetrahedrals or hexahedras. The size of these elements is a crucial parameter, as a finer mesh results in a more accurate approximation of the solution, while a courser mesh reduces the computational time.

All the single elements Ω_h together form assembly Ω_t. Due to the simple shape of the elements Ω_t does not perfectly correspond to the real domain Ω, creating an inaccuracy in the final approximated solution, which depends once again on the meshing density.

In each subdomain, due to the meshing, a number of nodal points are defined. These nodal points are the supporting points of the basis functions φ_a(x). The basis functions φ_a(x), implemented for the approximated functions, are low order polynomials and the order is chosen according to the desired accuracy.

As an example, we consider a 1D domain divided into elements of small intervals [x_n-1,x_n] with n = 1,…,M, where x_n are the nodes. The following proprieties have to be satisfied [48]:

Nodal point are ordered
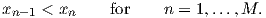$xn -1 < xn for n = 1,...,M.$ (2.116)
The domain is completely covered
$M⋃ [a,b] = [xn-1,xn] xo = a,xM = b. n=1$ (2.117)
Each interval is unique
$[xn- 1,xn]∩ [xk- 1,xk ] = ∅ for n ⁄= k.$ (2.118)

In order to simplify the example we use an equidistant discretization

xn = a+ nh n = 0,...,M,

where the mesh size h is defined by

a---b h = M .

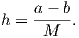(2.119)

The approximation function u_h(x) is then composed of a combination of linear functions that are non zero in a small interval. For example, if we consider piecewise linear hat-functions (Figure 2.7), defined by

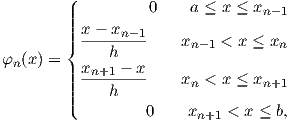( || 0 a ≤ x ≤ xn-1 |||| x - xn- 1 |{ --------- xn-1 < x ≤ xn φn (x) = | x h- x |||| --n+1---- xn < x ≤ xn+1 ||( h 0 xn+1 < x ≤ b,

(2.120)

then, on the nodal points, the chosen basis functions fulfill the conditions

{ 1 n = k φn (xk ) = δnk = 0 n ⁄= k

(2.121)

and the approximate function u_h(x) is defined by

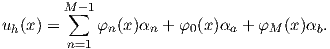M -1 u (x) = ∑ φ (x)α + φ (x )α + φ (x)α . h n=1 n n 0 a M b

(2.122)

This allows the calculation of the unknown parameters α_n by applying one of the methods previously described (cf. Section 2.6.1).

Figure 2.7: Piecewise linear hat-functions

The chosen polynomial functions have to be continuous over the entire domain.

2.7 FEM for Solid Mechanics

A typical application for FEM are solid mechanics problems. Here, a general derivation and implementation for a linear elastic solid is presented [36]. The description follows a general framework used to find solutions for problems in solid mechanics. Different approaches to construct the weak form, as well as expressions for the strain and the constitutive law, can be found in [36, 49].

Figure 2.8: An unformed body (left) and a deformed body (right).

The system depicted in Figure 2.8 is used as an example. The following properties and equations of linear elastic bodies have to be considered:

The shape of the body at the deformed configuration Ω.
The initial stress field in the body (zero in this FEM setting).
The elasticity tensor C (cf. (2.38)).
The coefficients of thermal expansion (2.48) for the body as well as the temperature distribution (to simplify the FEM derivation they are neglected).
A body force distribution b (force per unit volume) acting on the body.
Boundary conditions: displacement u(x_D) on a section Γ_D of the boundary Ω or tractions t_i on a section Γ_t of the boundary Ω.

The coefficients u_i, ε_ij, and σ_ij are calculated by satisfying the governing equations of static linear elasticity:

The Eulerian infinitesimal strain tensor (2.21).
The elastic stress-strain relation (2.37).
The equation of static equilibrium for stress (cf. (2.34)), given by ∂σ_ij∕∂x_i+ρb_i = 0.
Boundary conditions of the stress and the displacement: σ_ijn_i = t_i on Γ_t and u_i = u(x_D) on Γ_D.

In Section 2.4 we demonstrated how the virtual work is used to replace the stress equilibrium equations. The principle was expressed by defining a virtual displacement field δu(x). The principle of virtual work corresponds to the weak formulation of the equilibrium condition.

If σ_ij satisfies

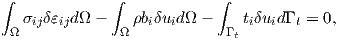∫ ∫ ∫ σ δε dΩ - ρb δud Ω- tδu dΓ = 0, Ω ij ij Ω i i Γ ti i t

(2.123)

for all virtual displacement fields and virtual strains, the equation of stress equilibrium ∂σ_ij∕∂x_i + ρb_i = 0 and the boundary condition σ_ijn_i = t_i on Γ_t are automatically satisfied (cf. Section 2.4). By employing the principle of virtual work the displacement field in a linear elastic solid in an integral form (weak form) can be derived.

To better explain the FEM procedure the first integral in (2.123) can be rewritten. In fact, by employing the symmetry of the stress tensor σ_ij = σ_ji for the virtual strain definition (2.54) we can write

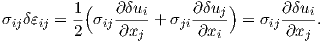1-( ∂δui- ∂-δuj) ∂δui- σijδεij = 2 σij∂xj + σji ∂xi = σij ∂xj .

(2.124)

Furthermore for linear elastic solids we recall σ_ij = C_ijklε_kl = C_ijkl(∂u_k∕∂x_l + ∂u_l∕∂x_k)∕2 and C_ijkl = C_ijlk, leading to σ_ij = C_ijkl(∂u_k∕∂x_l). This allows us to write

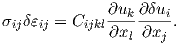∂uk ∂δui σijδεij = Cijkl∂x-∂x--. l j

(2.125)

The expression (2.125) can be plugged into the first term of (2.123) and the virtual work can be rewritten as

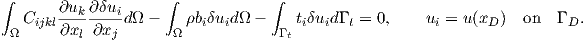∫ ∫ ∫ C ∂uk-∂δuidΩ - ρb δu dΩ - tδu dΓ = 0, u = u(x ) on Γ . Ω ijkl∂xl ∂xj Ω i i Γ t i i t i D D

(2.126)

The displacement field u_k(x) is solved if it satisfies (2.126) for all virtual velocity fields δu_i fulfilling δu_i = u(x_D) on Γ_D.

The strain components can be obtained from ε_ij = 1∕2(∂u_i∕∂x_j + ∂u_j∕∂x_i). By using the stress-strain relation σ_ij = C_ijklε_kl the stresses can be calculated. In this procedure no partial differential equations need to be solved; instead, equivalent integrals are present making the problem solvable using FEM.

The integral form of (2.126) can be approximated by discretizing the displacement field, which can be calculated as a set of n discrete points in the body, known as nodes. We denote them as x_i^a with a = 1,…,n; therefore, the unknown displacement vector at each node is denoted as u_k(x_i^a).

The FEM procedure specifies the displacement field at an arbitrary point within the solid by interpolating between nodal values. The interpolation function can be defined as

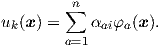n ∑ uk(x) = αaiφa(x). a=1

(2.127)

The same procedure can be used for the virtual displacement, which represents the test function

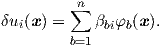∑n δui(x ) = βbiφb(x). b=1

(2.128)

Now (2.127) and (2.128) are substituted in (2.126). By choosing β_bi = δ_bb′,δ_ii′ for b′∈{1,…,n} and i′∈{1,…,3}, the virtual work equation can be expressed in a system of linear equations

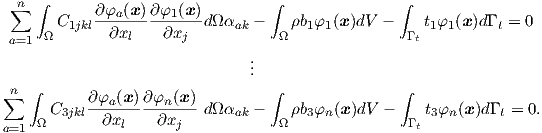n ∫ ∫ ∫ ∑ ∂-φa(x)∂-φ1(x) Ω C1jkl ∂xl ∂xj dΩ αak - Ω ρb1φ1(x)dV - Γ t t1φ1(x )dΓ t = 0 a=1 ... ∑n ∫ ∫ ∫ C3jkl∂-φa(x)∂-φn(x) dΩ αak - ρb3φn(x)dV - t3φn (x)dΓ t = 0. a=1 Ω ∂xl ∂xj Ω Γ t

(2.129)

The system of equations in (2.129) can be rewritten in matrix form as

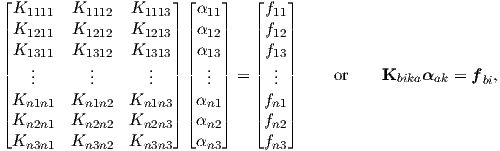⌊ K1111 K1112 K1113⌋⌊ α11⌋ ⌊f11⌋ || K1211 K1212 K1213|||| α12|| ||f12|| || K1311 K1312 K1313|||| α13|| ||f13|| || . . . |||| . || || . || || .. .. .. |||| .. || = || .. || or Kbikaαak = f bi, || Kn1n1 Kn1n2 Kn1n3 |||| αn1|| ||fn1|| ⌈ Kn2n1 Kn2n2 Kn2n3 ⌉⌈ αn2⌉ ⌈fn2⌉ Kn3n1 Kn3n2 Kn3n3 αn3 fn3

(2.130)

where the notations indicate

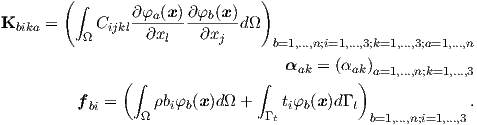( ) ∫ ∂φa (x)∂φb (x ) Kbika = Ω Cijkl--∂x-----∂x---dΩ l j b=1,...,n;i=1,...,3;k=1,...,3;a=1,...,n αak = (αak )a=1,...,n;k=1,...,3 (∫ ∫ ) f bi = ρbiφb(x)dΩ + tiφb (x )dΓ t . Ω Γ t b=1,...,n;i=1,...,3

(2.131)

Therefore, the α_ak parameters for the displacement u_k(x) can be obtained and, by using the elastic strain relations, the stress in the deformed body can be calculated.

[next] [prev] [prev-tail] [front] [up]

Chapter 2Overview of Solid Mechanics and the Finite Element Method