4.6.2 Scattering with Acoustic Phonons
Interaction with acoustic phonons (AP) can be
approximated as elastic scattering,
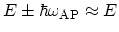 . As
discussed in Section 2.6, near the
. As
discussed in Section 2.6, near the 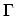 -point a linear dispersion
relation for acoustic phonons is assumed,
-point a linear dispersion
relation for acoustic phonons is assumed,
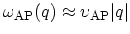 , where
, where
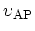 is the acoustic phonon
velocity. Furthermore, at room temperature low energy
phonons have an appreciable occupation, such that
is the acoustic phonon
velocity. Furthermore, at room temperature low energy
phonons have an appreciable occupation, such that
 |
(4.45) |
With equation (4.45) and the elastic approximation
the contributions due to phonon emission and absorption become equal and can
be lumped into one term. As a result, by using the relations (2.15) and (2.19)
the self-energies due to acoustic phonon interaction are written as
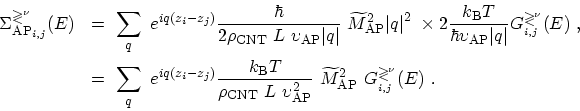 |
(4.46) |
With the exception of the exponential term all terms in (4.46) can be taken
out of the sum and one can convert the sum into an integral over q,
see (4.38) and (4.39). The self-energies simplify to
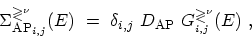 |
(4.47) |
where similar to (4.42)
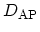 is given by
is given by
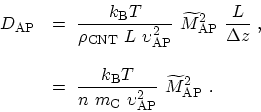 |
(4.48) |
A discussion similar to that in Section 4.6.1 gives a justification to keep
only diagonal elements of the self-energy due to the interaction
of electrons with acoustic phonons.
By substituting (4.47) in (3.76) the retarded self-energy
is obtained as
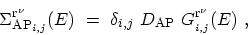 |
(4.49) |
Due to the approximations made the retarded self-energy for scattering with
acoustic phonons is simplified and directly related to the retarded
GREEN's function.Therefore, one does not need to evaluate the integrals
like (4.43), which implies a considerable saving of computational
cost.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors