4.6.1 Scattering with Optical Phonons
In this section the self-energies due to the interaction of electrons with
optical phonons (OP) are evaluated. As discussed in Section 2.6, the
phonon energy and the reduced electron-phonon matrix elements for OP
phonons are approximately constant and independent of the phonon wave-vector.
Under this assumption all terms except the exponential term
in (4.36) and (4.37) can be taken out of
the integral (4.38) and one obtains [55]
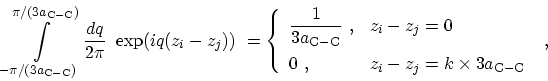 |
(4.39) |
where 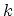 is an integer number. One has to multiply the above result by a
factor of
is an integer number. One has to multiply the above result by a
factor of 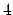 , for the number of rings in the lattice period [55].
Equation (4.39) justifies the approximation which only considers
diagonal elements of the electron-phonon self-energy. As discussed
in Section 4.3, by employing the nearest neighbor tight-binding method
(block) tri-diagonal matrices are achieved. Keeping only diagonal elements of
the electron-phonon self-energy, the matrices remain (block)
tri-diagonal. Therefore, an efficient recursive method (Appendix H) can
be used to calculate the inverse matrices. This implies
considerable reduction of computational cost and memory requirement.
, for the number of rings in the lattice period [55].
Equation (4.39) justifies the approximation which only considers
diagonal elements of the electron-phonon self-energy. As discussed
in Section 4.3, by employing the nearest neighbor tight-binding method
(block) tri-diagonal matrices are achieved. Keeping only diagonal elements of
the electron-phonon self-energy, the matrices remain (block)
tri-diagonal. Therefore, an efficient recursive method (Appendix H) can
be used to calculate the inverse matrices. This implies
considerable reduction of computational cost and memory requirement.
Using the result of (4.39) and the relations (2.15)
and (2.19) the self-energy due to scattering with optical phonons can be written as
![\begin{displaymath}\begin{array}{l}\displaystyle \Sigma_{\mathrm{OP}_{i,j}}^{<^\...
...G_{_{i,j}}^{<^\nu}(E-\hbar\omega_\mathrm{OP}) ] \ , \end{array}\end{displaymath}](img845.png) |
(4.40) |
![\begin{displaymath}\begin{array}{l}\displaystyle \Sigma_{\mathrm{OP}_{i,j}}^{>^\...
...G_{_{i,j}}^{>^\nu}(E+\hbar\omega_\mathrm{OP}) ] \ , \end{array}\end{displaymath}](img846.png) |
(4.41) |
where
 is given by
is given by
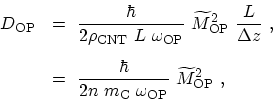 |
(4.42) |
where
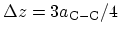 (see (4.3)).
In the second line in (4.42) the
mass density of a
(see (4.3)).
In the second line in (4.42) the
mass density of a 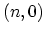 zigzag CNT has been replaced
zigzag CNT has been replaced
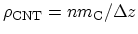 , where
, where
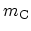 is the mass of a
carbon atom.
is the mass of a
carbon atom.
The retarded self-energy can be calculated as (3.76)
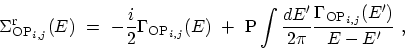 |
(4.43) |
where
![\begin{displaymath}\begin{array}{l}\displaystyle \Gamma_{\mathrm{OP}_{i,j}}(E)=i...
...m} [\Sigma^\mathrm{<}_{\mathrm{OP}_{i,j}}(E)] \ . \ \end{array}\end{displaymath}](img852.png) |
(4.44) |
Since the lesser and greater self-energies are assumed to be diagonal the
retarded self-energy is also diagonal.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors