


Prev: 5.3 Coupling with Lithography
Up: 5.3 Coupling with Lithography
Next: 5.3.2 Contact Hole Printing
5.3.1 Lithography Modeling
Optical lithography is a complex process determined by many chemical and
physical effects. As indicated in Fig. 5.5, a rigorous model for the
simulation of photo-lithographic exposure has to include many cross-related
quantities. The concentration of the photo-active compound
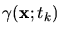 changes with the incident light intensity
changes with the incident light intensity
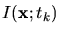 and determines the optical properties of the resist, such
as the permittivity
and determines the optical properties of the resist, such
as the permittivity
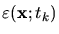 and the refractive index
and the refractive index
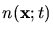 . Hence, the electro-magnetic phasor
. Hence, the electro-magnetic phasor
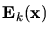 has to be
calculated inside an inhomogeneous medium. The absorbed light intensity
retro-acts on the concentration of the photo-active compound, which requires an
iterative solution
has to be
calculated inside an inhomogeneous medium. The absorbed light intensity
retro-acts on the concentration of the photo-active compound, which requires an
iterative solution
Figure 5.5:
Simulation flow of the exposure/bleaching module. The chemical state of the
photo-resist is described by the concentration
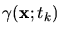 of the
PAC. The optical properties, e.g., the permittivity
of the
PAC. The optical properties, e.g., the permittivity
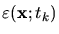 of the resist, depend on
of the resist, depend on
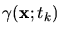 . Hence the EM field phasor
. Hence the EM field phasor
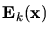 has to be calculated inside an inhomogeneous medium. With the absorbed light
intensity
has to be calculated inside an inhomogeneous medium. With the absorbed light
intensity
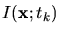 the concentration
the concentration
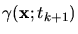 for the next time-step
for the next time-step 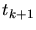 can be derived.
can be derived.
![\begin{figure}\psfrag{gxt}{\large$\gamma(\mathbf{x};t_k)$}\psfrag{ext}{\large$\v...
...ludegraphics[width=0.95\textwidth]{eps-dev/EXflow.eps}}
\end{center}\end{figure}](img219.gif) |
The crucial point throughout lithography simulation is the solution of the
Maxwell equations. Several methods for the numerical solution of the Maxwell
equations have been proposed, ranging from simple vertical scalar models to
rigorous approaches based on FEM discretizations of the Maxwell equations. We
have used a three-dimensional extension of the differential
method [32], which will be recapitulated in the following.
As can be seen from Fig. 5.5, the absorbed light intensity
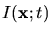 inside the optically nonlinear resist has to be determined.
The exposure state of the photo-resist is described by the concentration of the
photo-active compound
inside the optically nonlinear resist has to be determined.
The exposure state of the photo-resist is described by the concentration of the
photo-active compound
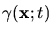 . Dill's
``ABC''-model [9] is used for the correlation between the exposure
intensity
. Dill's
``ABC''-model [9] is used for the correlation between the exposure
intensity
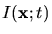 and the bleaching of the resist, which determines
the change in the resist's refractive index
and the bleaching of the resist, which determines
the change in the resist's refractive index
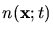
where 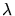 is the wavelength used for the exposure. This relation requires
the knowledge about the intensity distribution which has to be calculated from
the solution of the Maxwell equations. Assuming a time-harmonic field
distribution within a time-step
is the wavelength used for the exposure. This relation requires
the knowledge about the intensity distribution which has to be calculated from
the solution of the Maxwell equations. Assuming a time-harmonic field
distribution within a time-step
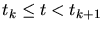 , the EM field obeys the
Maxwell equations in the form
, the EM field obeys the
Maxwell equations in the form
Due to the spatially periodic nature of the incident light and the assumption
of a laterally periodic simulation domain the EM field inside the simulation
domain can be expressed by a Fourier expansion
The permittivity itself is related to the refractive index by Maxwell's
formula
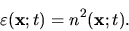 |
(5.7) |
Additionally, the inhomogeneous permittivity
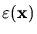 and its reciprocal
and its reciprocal
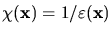 can be expanded in Fourier series
can be expanded in Fourier series
Insertion of (5.6) and (5.8) into
(5.5) transforms the partial differential
equations (PDE) into an infinite-dimensional set of coupled ordinary
differential equations (ODE) for the Fourier coefficients of the lateral field
components.
For the numerical solution of the equation system, the application of
appropriate boundary conditions is necessary. Above the simulation domain we
have to consider incident and reflected waves, whereas below only outgoing
waves occur. The incident light is known from the aerial image
simulation, whereas the unknown reflected and outgoing
fields are eliminated by applying radiation boundary conditions. The resulting
boundary value problem is solved by a numerically efficient implementation of
the shooting method [31] which supplies the EM field coefficients.
The EM field coefficients are transformed back to the spatial
domain and the solution of the EM field intensity
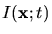
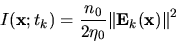 |
(5.9) |
for the time-step 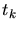 is obtained. In case of strongly bleaching resists
this process has to be repeated until the total exposure dose is reached.
is obtained. In case of strongly bleaching resists
this process has to be repeated until the total exposure dose is reached.
Because the bleaching rate
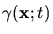 is almost negligible when
compared with the frequency of the EM field, the refractive index
is almost negligible when
compared with the frequency of the EM field, the refractive index
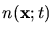 varies only slowly with respect to the field propagation and
thus a quasi-static approximation
varies only slowly with respect to the field propagation and
thus a quasi-static approximation
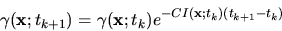 |
(5.10) |
can be applied to (5.4).
The inhomogeneous PAC concentration can be derived from this expression. As
last step, we use Kim's ``R''-model [29] to relate the
PAC distribution to a spatially inhomogeneous development rate.
The numerical values of the development rate are given
on a tensor product grid which is used for the representation of the optical
properties of the simulated structure. If the spacing of the grid is the same
as the cell size used for the topography simulation, the rates can be
transfered directly to the cellular structure, otherwise the rates have to be
interpolated. In the following section this simulation approach will be applied
to the printing of a contact hole over different substrates.



Prev: 5.3 Coupling with Lithography
Up: 5.3 Coupling with Lithography
Next: 5.3.2 Contact Hole Printing
W. Pyka: Feature Scale Modeling for Etching and
Deposition Processes in Semiconductor Manufacturing
![\begin{figure}\psfrag{gxt}{\large$\gamma(\mathbf{x};t_k)$}\psfrag{ext}{\large$\v...
...ludegraphics[width=0.95\textwidth]{eps-dev/EXflow.eps}}
\end{center}\end{figure}](img219.gif)
![\begin{figure}\psfrag{gxt}{\large$\gamma(\mathbf{x};t_k)$}\psfrag{ext}{\large$\v...
...ludegraphics[width=0.95\textwidth]{eps-dev/EXflow.eps}}
\end{center}\end{figure}](img219.gif)
![]() inside the optically nonlinear resist has to be determined.
The exposure state of the photo-resist is described by the concentration of the
photo-active compound
inside the optically nonlinear resist has to be determined.
The exposure state of the photo-resist is described by the concentration of the
photo-active compound
![]() . Dill's
``ABC''-model [9] is used for the correlation between the exposure
intensity
. Dill's
``ABC''-model [9] is used for the correlation between the exposure
intensity
![]() and the bleaching of the resist, which determines
the change in the resist's refractive index
and the bleaching of the resist, which determines
the change in the resist's refractive index
![]()
![]() and its reciprocal
and its reciprocal
![]() can be expanded in Fourier series
can be expanded in Fourier series
![]()
![]() is almost negligible when
compared with the frequency of the EM field, the refractive index
is almost negligible when
compared with the frequency of the EM field, the refractive index
![]() varies only slowly with respect to the field propagation and
thus a quasi-static approximation
varies only slowly with respect to the field propagation and
thus a quasi-static approximation
![]()
![]()
![]()
![]()