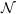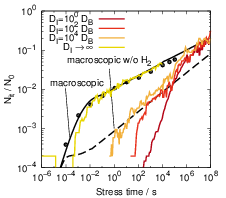3 A Microscopic Reaction-Diffusion Model for NBTI
As mentioned in Chap. 1, the reaction diffusion model has been mainly used for the interpretation of
BTI experiments for almost four decades. Its apparent inability to explain NBTI recovery has led to
several modifications of the concept, including trapping of the diffusing species and different types of
diffusors [11, 9].
Quite recently it was claimed that the misprediction of recovery is due to the one-dimensional
description of the diffusing species in the macroscopic model (1.5)–(1.6). As illustrated in Fig. 3.1, it
was suggested that this formulation makes it too easy for the hydrogen atom to find a dangling bond
to passivate because the one-dimensional diffusion considers only two options of motion: forward and
backward jumping. In a higher-dimensional description the diffusion and reaction kinetics are much
richer:
- The atoms can move in all three dimensions equally likely, leading to a distribution of
arrival times at the interface during recovery.
- H2-molecules dissociate at a dangling bond, creating a passivated dangling bond and a
free hydrogen atom that does not immediately find another dangling bond to passivate.
- Hydrogen atoms arriving later have to hover along the interface to find an unoccupied
dangling bond.
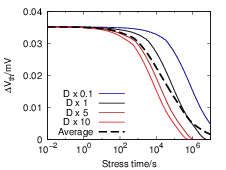
A simple estimate of the recovery in the hypothetical three-dimensional model is given in [16]. This
estimate mimics the different repassivation kinetics arising in the atomic description within the
framework of the usual macroscopic RD model. To account for the longer “effective” recovery
paths, the diffusion coefficients in the macroscopic model are reduced by different factors
during recovery and the resulting recovery traces are averaged. Although this approach
gives a recovery that proceeds over more time scales, as shown in Fig. 3.2, no derivation
for the quasi-three-dimensional description is given and its physical validity is at least
questionable. One of our targets is to test the claims of [16] within a firm theoretical
framework.
Another motivation for the study of the microscopic limit of the reaction-diffusion model for NBTI
is based on general issues with the rate-equation-based description. As a literature study reveals,
reaction-diffusion systems have been studied in numerous scientific communities from both the
theoretical and the experimental side for more than a century [145, 146, 147, 148, 149, 150, 151].
Although the mathematical framework of the RD model (1.4)–(1.6) seems physically sound
and the description using densities and rate equations is commonly considered adequate,
it is a well known and experimentally confirmed result of theoretical chemistry that the
partial differential equation based description of chemical kinetics breaks down for low
concentrations [145]. Additionally, in reaction-diffusion systems bimolecular reactions, such as the
passivation and the dimerization reaction, require a certain proximity of the reactant species,
termed reaction radius [146, 151]. Usually the elementary bimolecular reactions happen
almost instantaneously and it is the required collision, i.e. the reduction of the distance
between two reactants below the reaction radius, which is the rate limiting step [145]. In
chemical kinetics, these reactions are called diffusion-limited or diffusion-controlled reactions
[147].
It is easy to show that diffusion must play a dominant role in the bimolecular reactions in the RD
model for NBTI. Fig. 3.3 schematically shows a uniform random distribution of dangling bonds on
a silicon (100) surface that corresponds to a density of 5 × 1012cm-2, which is a usual
assumption for N0 [45, 20, 23] in (1.1) or (1.4). The average distance between two nearest
neighbors at this density is d = N0-1∕2 ≈ 4.5nm. An atomic model of the Si-SiO2 interface
as in Fig. 3.4 shows that two points separated by this distance have a large number of
atoms in between. The assumption of an elementary reaction over this distance is clearly
inappropriate, so any reaction between particles of this separation must involve a diffusive
step.
Once established by the atomic viewpoint above, the diffusive influence on the bimolecular reactions
leads to contradictions in the RD model and its physical interpretation. The predicted degradation of
the RD model that is compatible with experimental data is only obtained if the hydrogen atoms
that are liberated during stress compete for the available dangling bonds and dimerize
at a certain rate. Both requirements involve diffusion over distances much larger than
the nearest neighbor distance, which takes about two seconds at a commonly assumed
diffusion coefficient of D = 10-13cm2∕s [20, 23]. The reaction radius ρH of the dimerization
reaction can be estimated from the Smoluchowski theory for irreversible bimolecular reactions
[146, 148, 149]
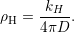 | (3.1) |
While a reasonable reaction radius is in the regime of the average radius of the oxide interstitials,
which is about 4Å [152], the application of (3.1) to published dimerization rates gives values ranging
from 70μm for the parametrization of [23] to thousands of kilometers for other parametrizations
[20]. Although both values for ρH seem quite unreasonable, they only indicate a limited physical
validity of the selected parametrization. An evaluation of the physical validity of the reaction-diffusion
model itself requires a more detailed study using a computational model that properly treats the
stochastic chemical kinetics involved.
For the present study of the microscopic properties of the RD mechanism we have developed our
own atomistic reaction-diffusion simulator based on the considerations of the previous chapter. The
microscopic reaction-diffusion picture developed for this purpose also serves as a framework to assess
whether a description based on rate-equations is applicable to the physical mechanism behind the RD
model.
3.1 The Microscopic RD Model
Our microscopic RD model attempts to mimic the proposed mechanisms of the reaction-diffusion
model at a microscopic level. The basic actors are H-atoms, H2-molecules and the silicon dangling
bonds at the interface. The level of physical detail in our model is chosen so that the single-particle
effects are captured in a physically meaningful way while still keeping the computational effort
manageable even for long-term simulations. Atomic vibrations, i.e. the microstate dynamics, are
certainly not of interest here. The present study concerns the RD-process itself and the
conclusions therefore do not depend on the microscopic details of the reactions at its basis.
The microscopic investigations are thus carried out at the stochastic chemistry level (see
Chap. 2).
Several algorithms have been used in the chemical literature for the stochastic simulation of
reaction-diffusion systems [148, 149]. The most difficult task in the modeling of these systems
is the diffusion of the reactants and several different approaches are available which can
roughly be categorized as grid-based methods or grid-less methods [149], see Fig. 3.5.
Grid-less methods propagate the coordinates of the diffusing species quite similarly to molecular
dynamics methods. Instead of explicitly treating all atoms of the solvent and their effect on the
trajectory of the diffusors, the motion of the diffusing particles is perturbed by an empirical random
force to generate a Brownian motion. Bimolecular reactions happen at a certain rate as soon as two
reaction partners approach closer than a given radius. Although this technique suffers from its
sensitivity to the time-step and the specific choice of the random force, it is a popular choice for the
simulation of reaction-diffusion processes in liquid solutions where real molecular-dynamics
simulations are not feasible [148, 149]. In grid-based methods the simulated volume is
divided into small domains and each diffusing particle is assigned to a specific domain. The
motion of the diffusors proceeds as hopping between the grid-points. In these models the
bimolecular reactions happen at a certain rate as soon as two reactants occupy the same
sub-volume. The advantage of this approach is that it can be formulated on top of the
chemical master equation (2.20). The master equation can then be solved using the stochastic
simulation algorithm (see Sec. 2.11), which does not depend on artificial time-stepping. A
problem of the grid-based method that is repeatedly discussed in chemical literature is the
choice of the spacial grid as it induces a more or less unphysical motion in liquid solutions.
Additionally, the probability to find two particles in the same grid point and in consequence
the rate of bimolecular reactions are quite sensitive to the volume of the sub-domains
[149].
In the reaction-diffusion model for NBTI, the diffusion of the particles proceeds inside a solid-state
solvent. Contrary to diffusion in gases or liquids, the motion of an impurity in a solid-state
host material proceeds via jumps between metastable states as illustrated in Fig. 3.6.
This hopping diffusion is understood as a barrier-hopping process as explained in Sec. 2.8. In the
case of H or H2, which do not react with the host atoms, the barriers arise from the repelling
Coulomb-interaction between the electron clouds of the host lattice and the diffusor. The minima of
the potential energy surface are thus the interstitial positions of the host lattice [59, 153]. In between
the jumps, the motion of the atom is randomly vibrational rather than diffusive or, in terms of
Chap. 2, a microstate trajectory. This discreteness of motion not only strongly suggests the
use of a grid-based method, where the grid points are interstitial positions of the host
lattice, it also induces a natural discretization into the reaction-diffusion equations. As a
consequence, the description based on macroscopic diffusion equations in the RD model (1.5)–(1.6)
are only valid at distances that are much larger than the interstitial radius and it has
to be assumed that at very short distances a description using hopping diffusion is more
accurate.
We conclude that the most appropriate description of the physics considered in the present work is
obtained from the reaction-diffusion master equation approach [151, 150, 148, 149]. Within the
natural lattice of interstitial positions the actors of our RD system exist in well-defined and discrete
states. In accord with the considerations of Sec. 2.6, it is now possible to define a state vector  that
contains the interstitial positions and bonding states of all actors as well as a set of reaction channels
which cause transitions between the states of this vector. The RD system then becomes a
time-dependent stochastic process
that
contains the interstitial positions and bonding states of all actors as well as a set of reaction channels
which cause transitions between the states of this vector. The RD system then becomes a
time-dependent stochastic process 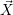 (t) that exists in one of a countable set of states
(t) that exists in one of a countable set of states 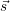 ω
and whose evolution over time can then be described by the chemical master equation
(2.20). As explained in Sec. 2.6, the physics behind the reaction channels are contained in
the propensity functions aγ and the state-change vectors
ω
and whose evolution over time can then be described by the chemical master equation
(2.20). As explained in Sec. 2.6, the physics behind the reaction channels are contained in
the propensity functions aγ and the state-change vectors 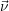 γ, which are given in Fig. 3.7.
The reactions employed in our simulations are the hopping transport between interstitial
sites, the passivation/depassivation reaction and the dimerization/atomization reaction.
γ, which are given in Fig. 3.7.
The reactions employed in our simulations are the hopping transport between interstitial
sites, the passivation/depassivation reaction and the dimerization/atomization reaction.
The stochastic chemical model is solved using the stochastic simulation algorithm (SSA) explained
in Sec. 2.11.
In the microscopic RD model employed in this work the interstitial sites form a regular and
orthogonal three-dimensional grid and the hopping rates for the diffusors are assumed to be constant
in accord with the isotropic and non-dispersive diffusion underlying the conventional macroscopic RD
model [9]. In a real SiO2 of a MOS transistor the amorphous structure will of course lead to a random
network of interstitial sites [152] with a variety of hopping rates and a more complex topology.
However, as the power-law degradation predicted by the macroscopic RD model requires a
constant diffusion coefficient, these variations must be assumed unimportant [22] in order to
obtain agreement with the established model. As illustrated in Fig. 3.8, the simulation
region in our calculations is a rectangular box which extends to infinity normal to the
Si-SiO2 interface and has closed lateral boundaries. The Si-SiO2 interface itself is represented by
a special region at the bottom of the simulation box where selected interface sites have
the ability to bond or release a diffusing hydrogen atom, see Fig. 3.7 and Fig. 3.8. The
positions of the dangling bond sites in the interface region are picked randomly, similar to
Fig. 3.3.
As mentioned above, the choice of the grid size requires special attention as it determines the
probability of the bimolecular reactions. The interstitial size of amorphous silica has been calculated
for molecular-dynamics generated atomic structures and is about 4Å [152]. We take this value as the
physically most reasonable grid size.
Once the microscopic model is defined, the relation to the macroscopic RD model (1.4)–(1.6) has to
be established. Using the number of dangling bonds in the simulation box nDB, the number of
hydrogen atoms passivating a dangling bond np and the numbers nHi of H and nH2i of
H2 at interstitial i, this relation is obtained from the discretization induced by the grid [23]
as
| N0 | = 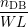 , , | (3.2)
|
| Nit | = 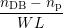 , , | (3.3)
|
| H(xi) | = 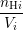 , , | (3.4)
|
| H2(xi) | = 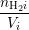 , , | (3.5) |
where W, L and h are illustrated in Fig. 3.8 and V i is the volume of interstitial i which is V i = h3 in
this work. The relation between the rates of the macroscopic model and the microscopic propensity
functions are given in Fig. 3.7. Initially, all hydrogen atoms are passivating silicon dangling
bonds
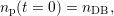 | (3.6) |
in accordance with the assumptions of the macroscopic RD model.
3.2 Results and Discussion
Two different systems have been studied in detail: a model system and a “real-world-example”. The
model system is used to study the general features of the microscopic reaction-diffusion process. It is
parametrized in order to clearly show all relevant features at a moderate computational effort. The
parametrization of the real-world system is based on a published parametrization of the modified
reaction-diffusion model. This system is used to relate our microscopic model to published
data.
3.2.1 General Behavior of the Microscopic RD Model
| Table 3.1:
| Parameters
of
the
model
system.
The
parameters
have
been
selected
to
enable
a
study
of
the
different
regimes
of
the
microscopic
RD
model
at
moderate
computational
expense.
The
rates
are
given
in
terms
of
the
microscopic
model
as
in
Fig. 3.7.
|
| Reaction | Propensity |
| | |
| Depassivation | 0.5s-1 |
| Passivation | 4 × 104s-1 |
| Dimerization | 2 × 105s-1 |
| Atomization | 5s-1 |
| H-hopping | 100s-1 |
| H2-hopping | 100s-1 |
The parametrization that is used to study the general behavior is given in Tab. 3.1. The number of diffusing
particles is a trade-off between accuracy and computational speed. Due to the large computational
demand ,
different regimes of the degradation curve have to be calculated with different numbers of diffusing
particles.
The earliest degradation times are dominated by the depassivation of the silicon dangling bonds
leading to a linear increase of the degradation, which is equivalent to the initial “reaction limited”
degradation of the macroscopic RD model [8]. However, the degradation predicted by the
microscopic RD model quickly saturates as an equilibrium forms between depassivation
and repassivation for each dangling bond separately. In absence of any diffusion the time
evolution of the number of hydrogen atoms passivating a silicon dangling bond is given
by
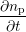 (t) (t) | = -kfnp(t) + 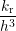 (nDB - np(t)) (nDB - np(t)) | (3.7)
|
| np(t = 0) | = nDB. | (3.8) |
with the solution
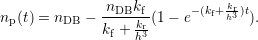 | (3.9) |
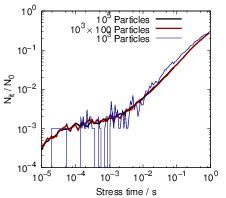
The main difficulty in the calculation of the early degradation times in the microscopic RD model is
the very low degradation level in this regime, which requires a high accuracy, i.e. a large number of
particles to obtain smooth results. Fortunately, as reactions between the hydrogen atoms or between
hydrogen atoms and neighboring dangling bonds are not happening in this regime, a good
parallelization can be obtained by averaging over separate simulation runs, see Fig. 3.9.
A comparison of the microscopic RD model and (3.9) is shown in Fig. 3.10.
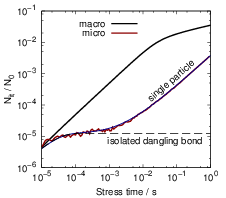
The initial behavior of the microscopic RD model stands in stark contrast to the degradation in the
macroscopic model where the linear regime continues until a global equilibrium has formed at the
interface.
As this initial behavior takes a central position in our further discussion, it requires a deeper
analysis. According to Sec. 2.12 the microscopic single-particle regime can be accurately
described using rate equations, as it does not contain any second-order reactions. The
required equations are basically those of the RD model, but as every hydrogen atom can be
assumed to act independently, the expressions for the hydrogen bonding as well as the
competition for dangling bonds are neglected. As the kinetic behavior in this regime is
strongly determined by the first diffusive steps of the hydrogen atoms, the diffusion part of
this approximation must have the same interstitial topology as the microscopic model. As
all hydrogen atoms act independently, only one atom and one dangling bond need to be
considered. The interface reaction and the diffusion of the hydrogen atom is thus described
as
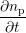 | = -kfnp + 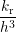 nDBnH0 and nDBnH0 and | (3.10)
|
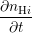 | = ∑
j∈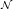 (i) (i)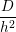 (nHj - nHi), (nHj - nHi), | (3.11) |
respectively, where 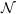 denotes the set of neighboring interstitials to i. Fig. 3.10 compares the
microscopic RD calculation with the approximations for the different regimes at early degradation
times, which shows that the single-particle model perfectly matches the behavior of the atomic model
in the initial phase.
denotes the set of neighboring interstitials to i. Fig. 3.10 compares the
microscopic RD calculation with the approximations for the different regimes at early degradation
times, which shows that the single-particle model perfectly matches the behavior of the atomic model
in the initial phase.
After the atoms have traveled sufficiently long distances, the interaction between the particles
becomes relevant and the single-particle approximation becomes invalid. In Fig. 3.11 this is visible as
a transition away from the single-particle behavior towards the macroscopic solution between 1s and
1ks. Due to the relatively large level of degradation, the long-term simulations do not require as much
accuracy as the short-term simulations. Consequently the number of particles can be reduced for
longer simulation times, which makes the prediction of long-term degradation possible.
Finally, Fig. 3.12 compares the microscopic RD model to the macroscopic version over the
course of one complete stress cycle, where the microscopic curve was obtained by combining
calculations of different accuracy, as explained above. Instead of the three regions which arise
from the macroscopic RD model — reaction-limited, equilibration and diffusion-limited —
the H-H2 microscopic description has four to five regimes depending on the particular
parametrization.
- The earliest degradation times (t < 20μs in this case) are dominated by the depassivation
of dangling bonds. In this regime, the microscopic and the macroscopic model give identical
degradation behavior.
- After the passivation and depassivation have reached an equilibrium between kf and
kr separately for each Si-H bond, the fraction of depassivated dangling bonds remains
constant until the diffusion of the hydrogen atoms becomes dominant. This regime only
shows when the individual hydrogen atoms are considered and consequently is not obtained
from any model based on rate equations.
- As more and more hydrogen atoms leave their initial position, the degradation is determined
by the buildup of a diffusion front along the Si-SiO2 interface and the equilibration
between the dangling bonds. This regime has a very large power-law exponent of almost
one
that is not experimentally observed. The stress time range in which this regime is observed
depends on the average distance between two dangling bonds, the diffusion coefficient and
the interstitial size.
- As the bimolecular reactions become relevant, the macroscopic diffusion-limited regime
begins to emerge. For some parametrizations we have observed a time window in which a
sufficient amount of H2 has not formed yet, and thus the initial diffusion-limited regime
has the typical t1∕4-form that arises from the classical RD model without H2 [25].
The initial single-particle phase of the degradation is a remarkable feature of the microscopic model.
As it is incompatible with experimental data and very sensitive to the parametrization, its relevance
for real-world reliability projections has to be investigated. For this purpose we have run calculations
based on a published parametrization of the reaction-diffusion model for NBTI, see Sec. 3.2.4.
3.2.2 Recovery
In agreement with our investigations on two-dimensional systems [25, 24], the three-dimensional
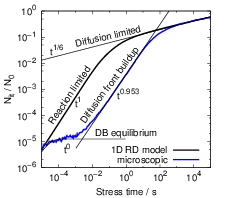
stochastic motion of the hydrogen atoms does not influence the recovery behavior of the system after
long-term stress, which contradicts the suggestions of [16]. As shown in Fig. 3.13, a longer relaxation
transient is only obtained if the foregoing stress phase does not show a power-law regime. As the
system comes closer to the macroscopic degradation behavior, the recovery in the microscopic
model also approaches the macroscopic version, which is incompatible with experimental
data [12, 154, 13]. This behavior is to be expected as the t1∕6 degradation regime requires
an equilibration and thus a quasi-one-dimensional behavior. The recovery proceeds on a
timescale that is at least two orders of magnitude longer than the stress time. The lateral
search of hydrogen atoms for unoccupied dangling bonds was suggested to dominate at
the end of the recovery. However, due to the logarithmic time scale on which recovery is
monitored, the equilibration along the interface has negligible impact at the end of the
recovery trace if this equilibration proceeds about two orders of magnitude faster. Thus, the
hovering of hydrogen atoms along the interface does not influence the shape of the recovery
transient.
3.2.3 Approximations in the Macroscopic Model
After the microscopic RD theory Fig. 3.7 has been established and its general behavior has been
investigated, one can use this framework to analyze the assumptions that are implicit to
the macroscopic RD model (1.4)–(1.6), which is still widely considered to be an adequate
approximation.
The most obvious approximation in the macroscopic RD model is the one-dimensional description of
diffusion. While this may seem to be appropriate as boundary effects in the diffusion of both H and
H2 are negligible, it tacitly introduces the assumption of lateral homogeneity along the interface. This
homogeneity includes the following assumptions:
- All the liberated hydrogen atoms at the interface (Hit in (1.1) and (1.4)) compete
instantaneously with all the other free interfacial hydrogen atoms for all the available
dangling bonds.
- All the pairs of hydrogen atoms at a certain distance from the Si-SiO2 interface are equally
likely to undergo dimerization and form H2, independently of their spatial separation.
As was shown above, a hydrogen atom liberated during stress initially stays in the vicinity of its original
dangling bond and thus the lateral homogeneity has to be considered a long-term approximation. It is
accurate when the diffusion of hydrogen has led to enough intermixing so that there is no significant
variability in the concentration of free hydrogen along the interface. Following [115] and
the discussion in Sec. 2.12, this condition can be called “lateral well-stirredness” of the
system.
The second and more delicate approximation in the macroscopic RD model is the mathematical
description using rate- and diffusion-equations. In the microscopic RD model, the rate at which an
atom at the interface passivates a dangling bond depends not only on the rate kr but also on the
probability of finding this atom at the position of the dangling bond. In the macroscopic
model the precondition of having an unoccupied dangling bond at the interface is described
multiplicatively as krNitHit. At early times during degradation, when each hydrogen atom
still resides near its dangling bond, this term introduces an unphysical self-interaction
where each hydrogen atom competes with itself for its dangling bond. As the root of this
problem lies in the assumptions implicit to a formulation based on rate-equations, the error is
also present in a macroscopic model with three-dimensional diffusion. As explained in
[25], this means that a rate-equation based RD model will not accurately describe the
degradation at early times even if higher-dimensional diffusion and discrete dangling bonds are
considered.
Similar to the passivation rate, the rate at which H2 is formed in the microscopic RD model
depends on both the dimerization rate kH and the probability of finding two hydrogen atoms which
occupy the same interstitial position. In the macroscopic RD model, this dimerization
reaction is modeled as kHH2. As thoroughly explained in [145], this approximation is
only valid for large numbers of particles, as the number of pairs of hydrogen atoms in an
interstitial goes as N(N - 1) which can only be approximated as N2 if N is sufficiently
large.
All in all, the macroscopic RD model can only be considered a valid approximation of the
microscopic RD model for very long stress times and a sufficient amount of liberated hydrogen atoms.
The time it takes for the macroscopic approximation to become valid, however, may exceed the time
range in which it is usually applied, depending on the parametrization.
3.2.4 A Real-World Example
| Table 3.2:
| The
parameters
employed
in
the
real-world
simulations.
The
parameter
set
is
based
on
the
values
published
in
[20]
but
was
slightly
modified
to
give
the
same
degradation
behavior
with
physically
more
reasonable
kr
and
kH.
|
| kf | 3 | s-1 |
| kr | 6 × 10-13 | cm3s-1 |
| kH | 5.6 × 10-11 | cm3s-1 |
| kH2 | 95.4 | s-1 |
| D | 10-13 | cm2s-1 |
| D2 | 1.8126 × 10-14 | cm2s-1 |
| N0 | 5 × 1012 | cm-2 |
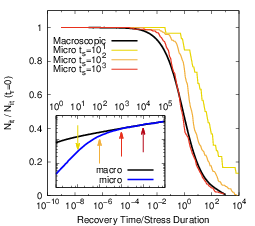
To study the behavior of the atomistic model for a real-world example, we compare to the
measurements of Reisinger et al. [12] using the parametrization of Islam et al. [20] in a modified
form, see Tab. 3.2. Fig. 3.14 shows the results of our calculations for several interstitial sizes. While
the macroscopic one-dimensional RD model fits the data very well, the kinetic Monte Carlo data
shows a completely different behavior. Again, the single-particle regime is clearly present. However,
due to the low density of dangling bonds at the interface, the single-particle regime dominates the
degradation for a large part of the stress time. For a realistic interstitial size of 4Å [152, 155], the
onset of the t1∕6 regime lies far beyond the experimental window of 105s. When the interstitial size is
increased, the onset of the t1∕6 regime moves to earlier times, which is due to the increase of the
reaction radius for the bimolecular reactions as explained above. For the given parameter set, an
interstitial size of h = 2nm, which is the total thickness of the oxide of the device under
consideration [12], is required to at least have the t1∕6 regime touch the experimental window.
A shift of the onset of the experimentally observed regime to earlier times at a realistic
interstitial size requires a dramatic increase of either the hydrogen diffusion coefficient or the
availability of free hydrogen near the interface. An increase of the hydrogen diffusion coefficient,
however, breaks the dominance of H2 flux over the flux of atomic hydrogen and changes the
predicted degradation away from the experimentally observed t1∕6 towards t1∕4. Increasing
the availability of hydrogen at the interface by adjusting the ratio kf∕kr causes similar
problems, as the H2 diffusion coefficient has to be lowered in order to give the same overall
degradation.
This indicates that in the given microscopic model it is impossible to obtain the experimentally
observed t1∕6 degradation within the experimental window at a reasonable interstitial size.
3.2.5 Increased Interface Diffusion
The behavior predicted by the microscopic model is completely incompatible with any experimental
data, while the description is much closer to the physical reality than the macroscopic RD model.
Only two interpretations are possible to resolve this dilemma. Either the ability of the macroscopic
RD model to fit degradation measurements has to be regarded as a mathematical artifact without
physical meaning, or the structure of the Si/SiO2 interface somehow accelerates the lateral
equilibration considerably. We investigated the second option more closely by considering
first-principles calculations that have shown a lowering of diffusion barriers for hydrogen (molecules)
along the Si∕SiO2-interface as compared to the bulk SiO2 [156]. These findings indicate that the
motion of hydrogen might proceed at a much higher rate at the interface. As a higher diffusivity at
the interface aids the lateral equilibration, it might be the sought process that makes the
one-dimensional RD model physically meaningful. To account for it in our microscopic model, we
applied different diffusion coefficients DI and DB in the interface region and in the bulk,
respectively.
As can be seen in Fig. 3.15, the increase of the interface diffusion coefficient accelerates the
degradation during the initial phase as it increases the transport of hydrogen atoms away from
their dangling bonds. Interestingly, even if the interface diffusion coefficient is increased by
four orders of magnitude there is no t1∕6 behavior visible, but instead the degradation
takes on the typical t1∕4 behavior of a hydrogen-only reaction-diffusion model. While the
competition for dangling bonds sets in earlier for increased interface diffusion coefficients, the
formation of H2 is not accelerated in the same way. Inspection of the atomic diffusion
shows that the acceleration of the dimerization is much less pronounced as the liberated
hydrogen atoms constantly leave the interface region into the bulk where the diffusion
proceeds slower and the collision rate is reduced. Only in the limit of DI →∞ will the
microscopic RD model match the experimentally observed behavior. Although these extremely
high interface diffusion coefficients lack any physical justification, this is still closer to the
physical reality than the assumption of immediate equilibration along the Si-SiO2-interface
at any depth that is inherent to the usually employed one-dimensional macroscopic RD
model.
As a side note we remark that in a real wafer, a nearly infinite diffusion coefficient along the
Si∕SiO2-interface would make the hydrogen spread out through the waver during stress. This would
again alter the degradation slope and give rise to cross-talk between neighboring devices that would be
measurable, but has never been reported.
3.3 Related Work
Three other scientific groups have put forward microscopic RD models recently [157, 23, 158] and
interestingly those investigations find a reasonable agreement between their microscopic description
and the macroscopic RD model. In the work of Islam et al. [23] the atomic description is basically
equivalent to the work presented here but is built upon a one-dimensional foundation which carries the
same implicit assumptions as the macroscopic model. Clearly this model cannot capture the effects
discussed in this chapter as those are solely due to higher-dimensional effects. From a physical point of
view, however, the one-dimensional approximation lacks justification considering the results presented
above.
The work of Choi et al. considers the three-dimensional diffusion of the particles based on a
grid-less stochastic formulation [158]. Although the degradation in that work seems to
match the macroscopic RD model quite well at first sight, also strong discrepancies arise
between the two for longer stress times. Interestingly, for situations where the approach
presented above predicts a degradation far below the prediction of the macroscopic model, the
degradation predicted by Choi et al. overshoots the macroscopic model considerably. Only for an
enormous density of dangling bonds or a very large reaction radius the macroscopic behavior is
obtained, in accord with our results. The degradation behavior in [158] initially follows
Nit(t) = kft, which suggests that the depassivated hydrogen atoms instantly leave the reaction
radius of their respective dangling bond. The following excessively high power-law exponent
suggests that the repassivation of the silicon dangling bonds is somehow inhibited in this
formulation. The most likely explanation for this behavior is a too low resolution of the
time-stepping, in combination with the physically unjustifiable description of the diffusive
motion.
The work of Panagopoulos et al. uses a grid-based stochastic RD model that seems to be
compatible with our description. The surprisingly good agreement between their results and the
macroscopic RD model may be an artifact of the employed method which is based on an adaptive
time-stepping [157]. Also, the paper states that the passivation reaction occurs if a hydrogen atom is
“close” to a dangling bond. This indicates an artificial capture radius, but this is not explicitly stated.
Also, the grid spacing is not given in the paper and its physical relevance is not discussed. However, as
shown by our calculations, an unphysically large grid spacing strongly promotes bimolecular reactions
and thus induces a degradation behavior that is (falsely) compatible with the macroscopic RD
model.
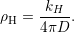

 that
contains the interstitial positions and bonding states of all actors as well as a set of reaction channels
which cause transitions between the states of this vector. The RD system then becomes a
time-dependent stochastic process
that
contains the interstitial positions and bonding states of all actors as well as a set of reaction channels
which cause transitions between the states of this vector. The RD system then becomes a
time-dependent stochastic process 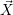 (
(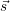
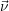
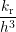
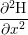
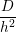
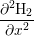
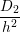
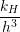
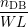
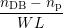
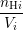
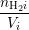
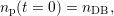
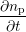 (
(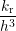 (
(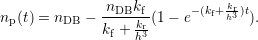
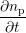
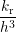
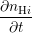
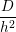 (
(