


 |  |  |
Drawing on considerations and abstracts of thinkers such as Thomas Aquinas and Descartes Newton was essential in formulating the stage from which to arrive at the abstraction of phase space. To this end it is important to recall that Newton formulates his famous three laws or axioms of motion:
He thus formulated the motion of bodies (or particles) focusing on the concept of forces
which are set in a space using an absolute time which is mathematically expressed as an
affine space 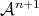 (Definition 79)
(Definition 79) 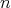 stands for the degrees of freedom and the additional
dimension is added to accommodate time. The absolute nature of time is modelled as a scalar
field
stands for the degrees of freedom and the additional
dimension is added to accommodate time. The absolute nature of time is modelled as a scalar
field

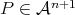 (symbolizing an event).
(symbolizing an event).

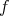 (Definition 61),
(Definition 61), 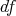 is constant in correspondence to
the absolute nature of time in Newton’s setting and defines a mapping
is constant in correspondence to
the absolute nature of time in Newton’s setting and defines a mapping

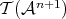 (Definition 48), which determines time spans between two events.
Furthermore, the kernel (Definition 22) of
(Definition 48), which determines time spans between two events.
Furthermore, the kernel (Definition 22) of 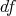 is an
is an 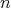 -dimensional Euclidean (Definition 80)
subspace
-dimensional Euclidean (Definition 80)
subspace 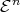 of
of 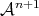 corresponding to all simultaneously occurring events. An affine space with this
additional structure is called a Galilean space [72]. A Galilean space has a natural fiber
bundle (Definition 40) structure of a one-dimensional base space (time), with
corresponding to all simultaneously occurring events. An affine space with this
additional structure is called a Galilean space [72]. A Galilean space has a natural fiber
bundle (Definition 40) structure of a one-dimensional base space (time), with 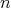 -dimensional fibers
(space) as is illustrated in Figure 5.1.
-dimensional fibers
(space) as is illustrated in Figure 5.1. Each of the fibers contains events which are said to occur at the same time. The evolution of an entity in
the affine space with the passing of time is represented as a section of this fiber bundle. While it
is simple to naturally denote a one-dimensional base space, with 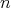 -dimensional fibers,
the reverse is not the case, as while time is defined as absolute, thusly globally defining
simultaneous events and thus fixed points in time, it is not clear what fixed points in space should
be.
-dimensional fibers,
the reverse is not the case, as while time is defined as absolute, thusly globally defining
simultaneous events and thus fixed points in time, it is not clear what fixed points in space should
be.
A transformation 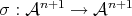 , which leaves the structure of a Galilean space invariant, is called
a Galilean transformation. Coordinate systems
, which leaves the structure of a Galilean space invariant, is called
a Galilean transformation. Coordinate systems

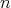 -dimensional subspaces and are called inertial. Galilean
transforms provide mappings between different inertial systems.
-dimensional subspaces and are called inertial. Galilean
transforms provide mappings between different inertial systems.
In this setting forces and the connected accelerations may be expressed as functions of the form:
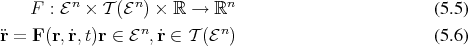
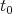 for the position
for the position 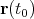 and
the velocity
and
the velocity 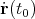 . Together with Newton’s three laws of motion a multitude of problems can already be
considered.
. Together with Newton’s three laws of motion a multitude of problems can already be
considered.
The relevance of Galilean transfoms is connected to the evolution of physical quantities in the system. The laws how to determine (measure) a quantity do not depended on time, thus the evolution of quantities is described by
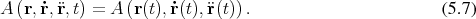
However, the formalism has been developed within the Cartesian setting of affine spaces. This leads to complications as the problems to which the formalism is applied increases in sophistication and adds complexity by being formulated directly in coordinate expressions. This leads to a strong mix of the representation in coordinates and the physical content, which is independent from the choice of coordinates. The search to overcome these limitations leads to a generalized reformulation of classical mechanics in the form of Lagrangian mechanics which recasts the single second order equation as two first order equations.
 |  |  |