


 |  |  |
Starting with Boltzmann’s equation in differential form

In addition to the trajectories, which are defined by the geometry of the phase space via the Hamiltonian
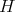 , it is also required to give a specific description of the collision operator on the right hand side. In
the field of semiconductor simulations it is common to describe the collision operator
, it is also required to give a specific description of the collision operator on the right hand side. In
the field of semiconductor simulations it is common to describe the collision operator 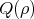 in the
form
in the
form
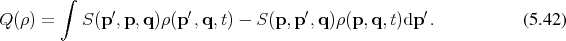

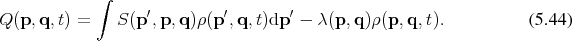
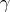 in phase space which provide a
mapping of a curve parameter to the phase space points, represented by the pair
in phase space which provide a
mapping of a curve parameter to the phase space points, represented by the pair 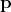 ,
, 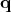 .
.
As such the expression for 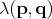 can also be rendered as
can also be rendered as 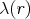 as a short form for
as a short form for
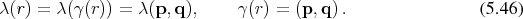
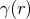 represents the trajectory travelled before a scattering event, while the particle continues to travel
on a trajectory
represents the trajectory travelled before a scattering event, while the particle continues to travel
on a trajectory 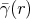 as indicated in Figure 5.3 afer a scattering event. With the two curves requiring to
match at the parameter
as indicated in Figure 5.3 afer a scattering event. With the two curves requiring to
match at the parameter 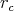 corresponding to a collision/scattering event in the following manner
corresponding to a collision/scattering event in the following manner
Utilizing these settings, Equation 5.42 can be rendered as
In the following the dependence of the curves 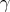 on the parameter shall be suppressed, where it
facilitates readability without adversely affecting clarity.
on the parameter shall be suppressed, where it
facilitates readability without adversely affecting clarity.
Here it is desirable to find an integrating factor, so that the left hand side resembles a total derivative. The integrating factor in this case is

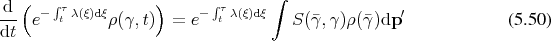
The last term deserves special consideration. It is easy to argue that it represents the initial conditions of
the sought function from which the system begins to evolve. It however also accommodates boundary
conditions as becomes apparent, when considering that the points of the trajectories corresponding to
the parameter  not necessarily lie within the domain of interest. In this case the trajectory within the
domain uses the value at the boundary instead as illustrated in Figure 5.4. Thus the term
accommodates both, initial as well as boundary conditions for this integral equation [92].
not necessarily lie within the domain of interest. In this case the trajectory within the
domain uses the value at the boundary instead as illustrated in Figure 5.4. Thus the term
accommodates both, initial as well as boundary conditions for this integral equation [92].
 |  |  |