


 |  |  |
So far little heed was paid to the number of entities under consideration as the formalisms are abstract
enough to deal with a scaling of the degrees of freedom. When considering 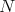 identical but
distinct entities in a three-dimensional setting, the associated phase space is simply a Cartesian
product (Definition 3) of the single phase spaces, thus forming an overall space of dimension
identical but
distinct entities in a three-dimensional setting, the associated phase space is simply a Cartesian
product (Definition 3) of the single phase spaces, thus forming an overall space of dimension 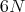 .
While the formalism does not hinder the specification of problems encompassing multiple entities, it
becomes increasingly difficult to obtain solutions. Furthermore, when turning to systems composed of
particularly large numbers of entities, such as molecules or atoms in gases, it becomes quite unfeasible
to deal with them directly, as the sheer amount of boundary and/or initial conditions becomes
prohibitive.
.
While the formalism does not hinder the specification of problems encompassing multiple entities, it
becomes increasingly difficult to obtain solutions. Furthermore, when turning to systems composed of
particularly large numbers of entities, such as molecules or atoms in gases, it becomes quite unfeasible
to deal with them directly, as the sheer amount of boundary and/or initial conditions becomes
prohibitive.
Therefore, a description offering a reduction of the overwhelming degrees of freedom is called for. This
can be demonstrated using a basic equation describing the evolution of 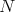 particles using a density
depending on the
particles using a density
depending on the 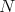 phase space coordinates and time
phase space coordinates and time

 , which depends on all of the particles.
, which depends on all of the particles.
By averaging by means of integration (Definition 94) an 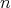 particle distribution function is
obtained
particle distribution function is
obtained
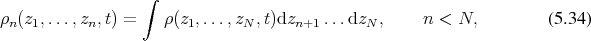

 appears as a fiber (Definition 40) over the reduced
phase space
appears as a fiber (Definition 40) over the reduced
phase space 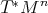 , since it is certain that
, since it is certain that
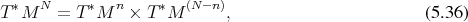
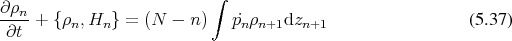
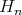 depends on the considered
depends on the considered 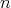 particles, while
the right hand side describes the interactions with all the remaining
particles, while
the right hand side describes the interactions with all the remaining 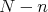 particles by
coupling to the next higher distribution function. Therefore this equation is not closed, but
gives rise to a hierarchy of equations, the BBGKY, named after the individuals who have
independently derived this system, Bogoliubov [87], Born [88], Green [89], Kirkwood [90] and
Yvon [91 ].
particles by
coupling to the next higher distribution function. Therefore this equation is not closed, but
gives rise to a hierarchy of equations, the BBGKY, named after the individuals who have
independently derived this system, Bogoliubov [87], Born [88], Green [89], Kirkwood [90] and
Yvon [91 ].
Using this formulation, the restriction to just one particle yields an expression for a single particle Hamiltonian, which results in phase space trajectories with deviations from these trajectories attributable to collisions.

While the derivation naturally describes the collison term with other particles, it can also model the interaction of the particle tracked by Boltzmann’s equation with the envrionment, thus allowing for an interpretation as probability of a particle evolving to a given point.
While Boltzmann’s equation appears as a simplification here, it is far from easy to obtain solutions to this deceivingly simple equation. Therefore several different techniques have been developed to at least calculate estimates in different contexts and with various levels of accuracy.
 |  |  |