| | |
While the description using Boltzmann’s equation is already a reduction with regard to the degrees of
freedom, it is still a statistical description on a microscopic level. It is important to be able to
link this modelling on a microscopic level to macroscopic quantities, which are accessible
to measurements. The statistical nature already offers a means in the form of expectation
values (Definition 101), which also allows to compact the statistics of the micro scale to
simple quantities of the macro scale. Thus, a macroscopic quantity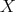 
on the manifold
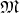(Definition 35) can be obtained from the microscopic description using 
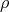on the phase space
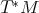by
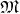(Definition 35),
indicating the powerful versatility of the fiber bundle abstraction.
An important feature of this prescription is that this procedure can not only be applied to
already obtained solutions of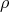 
as a post processing step, but can also be applied in order to
derive macroscopic equations from Boltzmann’s equation. Several differing procedures are
available to provide such a mapping resulting in differing macroscopic equations, ranging from
convection-diffusion, also called drift-diffusion, to the Euler equations or the Navier-Stokes equations.
This mapping may either be viewed as a defining derivation or as a link between two different
descriptions, which have been derived independently or have even been postulated by empiric
means.
A basic method uses a collection of weight functions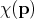 
to perform the contraction by
integrating (Definition 94) over sub-manifold slices formed by the momentum coordinates 
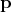. It thus
bears a certain resemblance to the procedure involved in the derivation of the BBGKY, except that the
integration is carried out only with respect to the momentum coordinate using the distribution as
measure, while preserving the spatial components.
| | |