


 |  |  |
Faced with severe difficulties of finding solutions of Boltzmann’s equation, Boltzmann himself was able
to derive the shape of the equilibrium state of the distribution 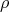 in the shape of the Maxwell-Boltzmann
distribution
in the shape of the Maxwell-Boltzmann
distribution

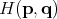 is the system’s Hamiltonian,
is the system’s Hamiltonian, 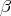 is connected to the average energy and thus
the temperature
is connected to the average energy and thus
the temperature 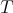 and
and  a factor additionally accounting for the number of degrees of
freedom.
a factor additionally accounting for the number of degrees of
freedom.
Furthermore, Hilbert’s investigations [124] of the dynamics of Boltzmann’s equations using an expansion into a power series of the form

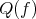 , and by extension
, and by extension 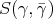 , is symmetric, the
evolution described by Boltzmann’s equation can be captured by using five distinct functions. These can
incidentally be linked to the macroscopic quantities of density, temperature and velocity. Thus
establishing that the evolution of systems described under these circumstances can be characterized
using hydrodynamic descriptions [124].
, is symmetric, the
evolution described by Boltzmann’s equation can be captured by using five distinct functions. These can
incidentally be linked to the macroscopic quantities of density, temperature and velocity. Thus
establishing that the evolution of systems described under these circumstances can be characterized
using hydrodynamic descriptions [124].
The interconnection between the theory of Boltzmann’s description and the macroscopic transport mechanisms becomes more apparent in lieu of the theory in Section 5.5, which allows to derive a series of macroscopic quantities as well as equations connecting these quantities and governing their evolution. In this context, Boltzmann’s statement regarding the shape of the equilibrium provides a guide for admissible assumptions during further derivations, while Hilbert’s theoretical result provides a strong argument how many quantities and hence equations must be considered.
When the conditions regarding symmetry are satisfied, the derivation of further quantities is not only not furthering the cause of obtaining better approximations, but on the contrary introduces unwarranted complications due to the computational effort which needlessly squanders resources. Thus the crunching of numbers can be reduced by employing information, which has been arrived at through completely theoretical means.
While Boltzmann conducted his research in the field of gas dynamics, his equation has found
applications beyond this initial field. One of these fields is the description of electron dynamics in
semiconductors. Where the scattering term in gas dynamics mainly considers interactions
between different particles, the case of semiconductors focuses on the interaction of an electron
with the surrounding semiconductor crystal. Thus, while in the field of gas dynamics the
energy contained in the gas can be considered a conserved quantity, especially if not
considering any boundaries, this is no longer appropriate in the case of solid state physics,
since the electrons interact with the crystal lattice and thus gain or remove energy form the
considered system. This necessitates a change in the symmetry of the scattering operator
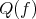 1.
1.
Since the symmetry considerations have been involved in the determination of the required number of equations, a reexamination of the previously sufficient set of equations is in order in this context. Thusly motivated, a ladder of equations has been derived following the scheme sketched in Section 5.5, which exceeds the previously established systems in complexity [126][127][128]. The complexity is further increased, as any system of equations derived from Boltzmann’s equation must be solved self consistently with a coupled Poisson equation, due to the charge of the involved particle. The involvement of charge, furthermore, leads to a doubling of effort, as positive and negative particles may be considered.
From among the derivable sets of equations the most widely used is also the simplest, which can also be easily derived on empirical considerations. The equations describe convection-diffusion, also called drift-diffusion, problem.
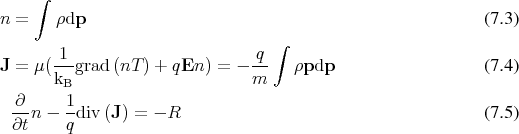
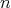 is
the number of electrons,
is
the number of electrons, 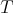 the temperature,
the temperature, 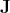 the electron current,
the electron current, 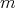 and
and 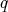 are the electron mass
and charge, respectively,
are the electron mass
and charge, respectively, 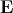 is the electric field, and
is the electric field, and 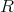 a term describing recombination with
holes.
a term describing recombination with
holes.
This model has been in use from early days of the semiconductor industry, when computational resources were far scarcer than they are today. For this reason it was of greatest importance for the applicability of this approach to develop a discretization scheme which maintains the level of accuracy with as coarse a spatial discretization as possible. Thus the computational effort has been considerably reduced, by accounting for the exponential distribution of electrons and at the same time consistently modelling the potential linearly [129].
Aiming to increase the accuracy of the physical description, the same discretization scheme has also
been applied to the equations derived using higher powers of 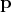 . This, however, is only of
limited success, as the increased computational effort is additionally coupled with problems of
obtaining a solution at all. Thus the more complex models have, so far, not found great adoption.
While the problems encountered in dealing with higher order transport models may very well
be attributed to their heightened complexity alone, it cannot be neglected that the applied
discretization scheme, which mimics the highly successful Scharfetter-Gummel discretization of
the drift diffusion model, is no longer consistent even in the case of a hydrodynamic, in
this context also often called energy transport, description. Thus as the physical models of
increasing complexity are additionally hampered by inconsistencies in their mapping from the
continuous to the digital world, numerical difficulties are hardly surprising. While these may be
unavoidable due to added degrees of freedom, even the most rigorous theoretical derivation of
models will be greatly handicapped and impaired, when the final translation to a discrete
setting is fragmented, especially in the unforgiving world of non-linear partial differential
equations.
. This, however, is only of
limited success, as the increased computational effort is additionally coupled with problems of
obtaining a solution at all. Thus the more complex models have, so far, not found great adoption.
While the problems encountered in dealing with higher order transport models may very well
be attributed to their heightened complexity alone, it cannot be neglected that the applied
discretization scheme, which mimics the highly successful Scharfetter-Gummel discretization of
the drift diffusion model, is no longer consistent even in the case of a hydrodynamic, in
this context also often called energy transport, description. Thus as the physical models of
increasing complexity are additionally hampered by inconsistencies in their mapping from the
continuous to the digital world, numerical difficulties are hardly surprising. While these may be
unavoidable due to added degrees of freedom, even the most rigorous theoretical derivation of
models will be greatly handicapped and impaired, when the final translation to a discrete
setting is fragmented, especially in the unforgiving world of non-linear partial differential
equations.
Despite the problems encountered in further refinement, the value of this approach to obtaining approximations to Boltzmann’s equation should not be neglected. Especially when considering the case of the drift-diffusion model, the required computational resources are comparatively modest compared to alternate methods of tackling the problem presented by Boltzmann’s equation.
 |  |  |