FEM simulations were carried out to understand the stress behavior in the TSV structure under the aforementioned conditions. For unfilled vias the meshing process is a challenging task. The thin layers of metal and oxide require a very fine mesh, in order to have a good approximation of the solution in those layers and in the regions surrounding them. Additionally, the cylindrical symmetry of the structure can be used to reduce the size of the problem, speed up the meshing process, and the simulation. In spite of that, one-quarter of the structure is employed in this section. The purpose of this increase in computational burden was to prepare the setup for the cases where the geometry symmetry can not be exploited, as will be seen in section 5.3.1.
Quadratic basis functions were used for the solution approximation and the BicGStab method for the linear solver [64]. Pre-conditioning is needed in order to obtain reliable results, especially in the case of the unfilled TSV, since the difference between the thin layers and the rest of the structure leads to scaling issues in the linear system. It is also possible to approach this problem by reducing the local meshing growth rate, but this would increase the size of the linear system and slow down the simulation.
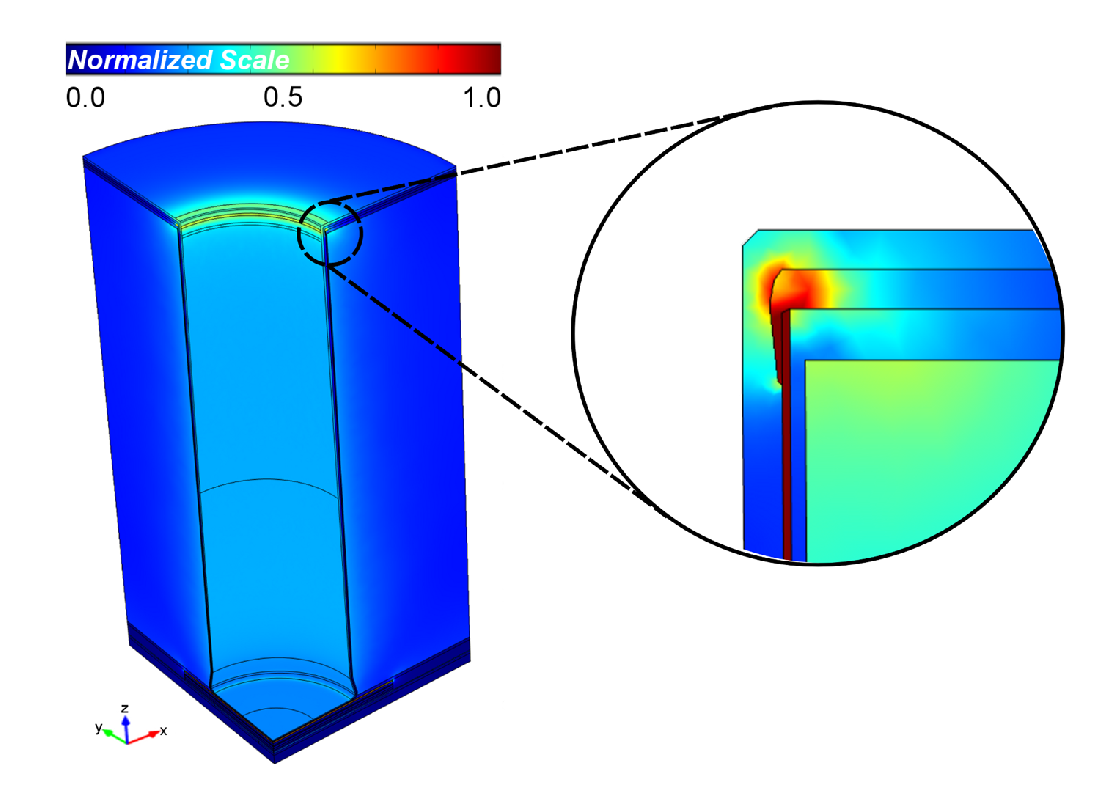
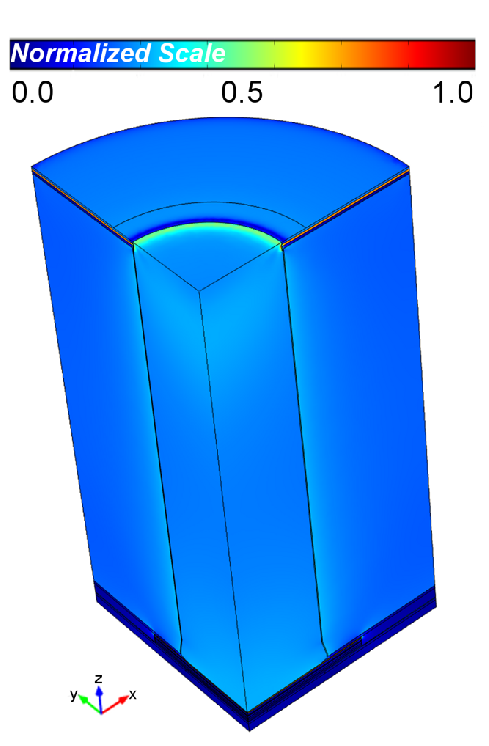
Von Mises stress plots are shown in Fig. 4.2 and Fig. 4.3 for the unfilled and the filled geometry, respectively. During thermal cycling, geometrical features influence the distribution of mechanical stress, especially on the top and the bottom of the via. One can see that the highest stress occurs in the metal layer at the bottom and near the top of the structures. In those regions the structures are under the influence of two factors: the thermal mismatch between the metal and the surrounding layers and the geometry. High mechanical stress in connection with microstructural properties, which weaken the stability of the crystal (dislocations, grain boundaries), can cause a fracture in the metal layers resulting in a complete failure of the TSV.
| Figure 4.2.: | Von Mises stress in the unfilled TSV. As depicted in the inset the top corner of the via is a point of high stress, especially in the oxide. Naturally, the metal sustains the highest stress in the structure. However, oxides are usually not as resistant to mechanical stress as copper or tungsten. The scale is normalized to the maximum stress obtained for this setup. |
| Figure 4.3.: | Von Mises stress in the filled TSV. The stress pattern is similar to the unfilled TSV (including the high stress spot at the top). However, the overall stress in the silicon is higher than the stress in the unfilled TSV. The scale is normalized to the maximum stress obtained for this setup. |
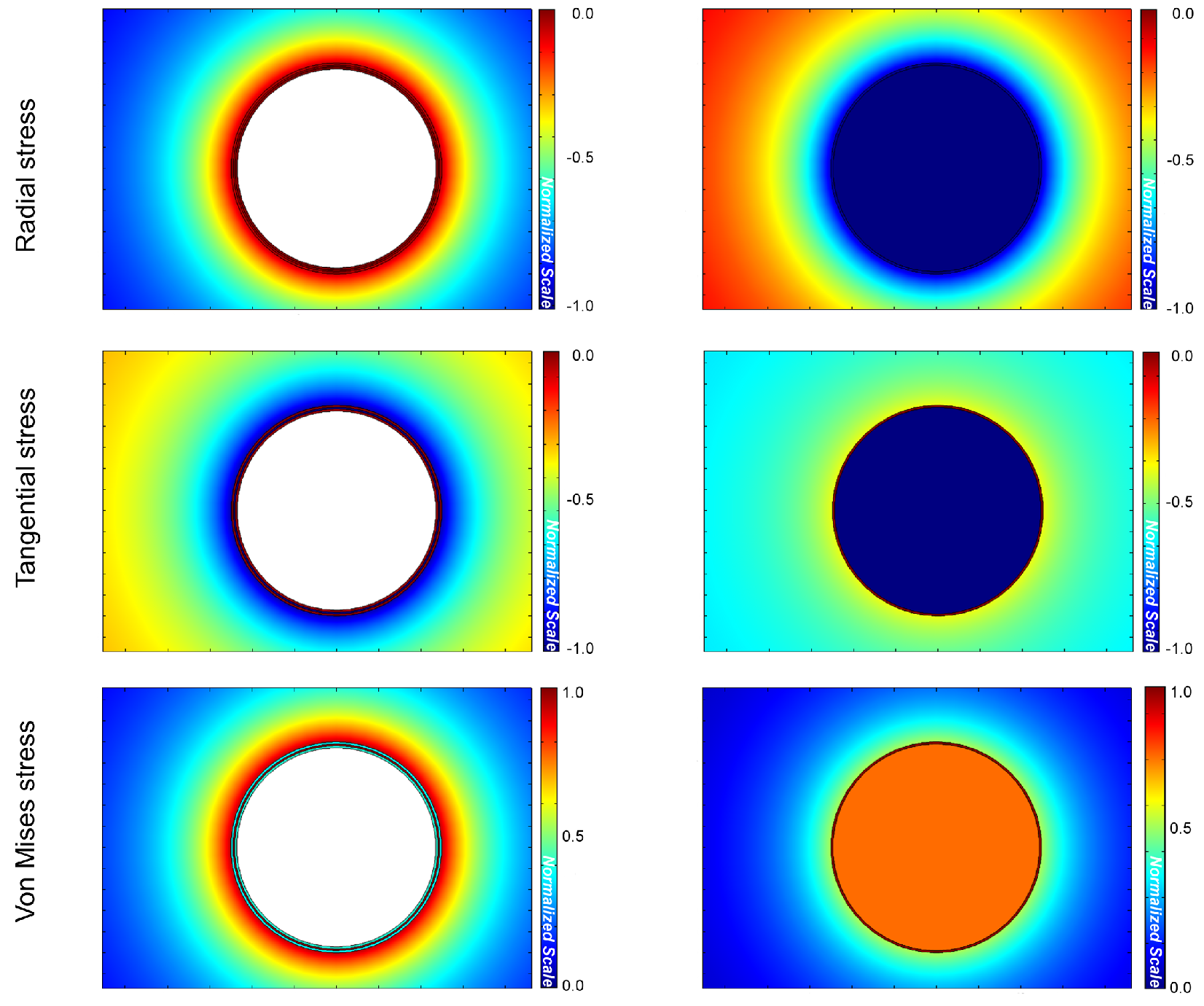
A two-dimensional cross section through the middle of the TSV provides a better view of the stress development through the silicon, as shown in Fig. 4.4. The stress distribution in the two designs are very similar in shape but not in magnitude.
| Figure 4.4.: | Stress fields in the unfilled TSV (left) and filled TSV (right). Cylindrical coordinates are used to simplify the analysis. |
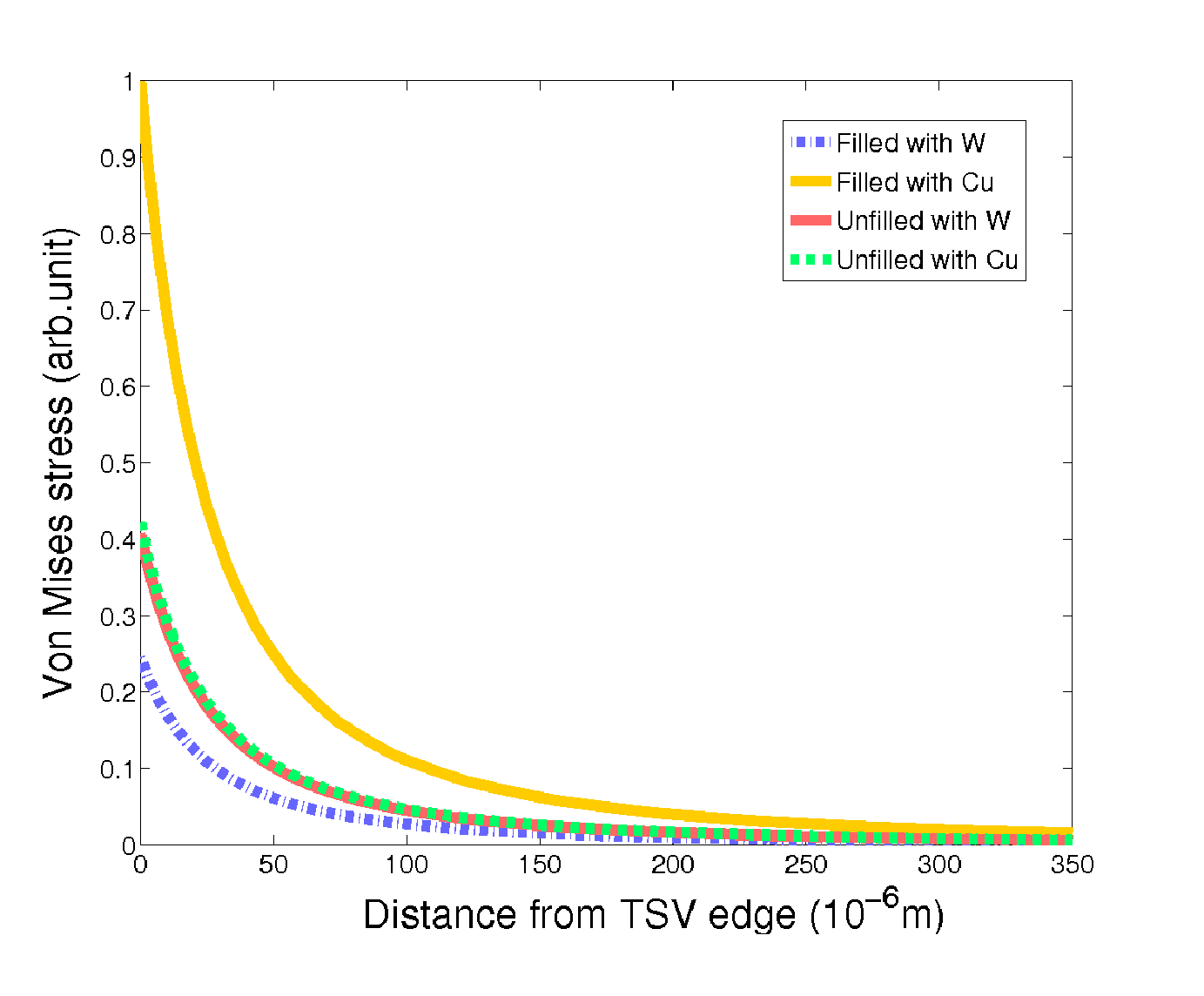
For both geometries the stress decays very quickly towards the silicon, but the mechanical advantage of one TSV over the other is highly dependent on the choice of metal present in the via. To clarify this argument, Fig. 4.5 shows the von Mises stress in the silicon along the radial direction, when copper or tungsten are considered as conductive metals.
| Figure 4.5.: | Von Mises stress through the silicon layer along the radial direction through the middle of the TSV height. For the unfilled TSV the choice of material is negligible for the stress level in the silicon. Most of the stress is produced by the geometry itself. In the filled TSV the metal plays a significant role. A large difference between the CTE of silicon and the metal creates high levels of stress, as shown by the Cu filled TSV. |
For unfilled TSVs the stress in the silicon is practically independent of the employed metal, due to the freedom of expansion toward the via’s middle axis. Actually, the stress induced by thermal variations on the surface of the open TSVs wall is essentially zero. In filled TSVs the situation is very different. The metal is constrained by the silicon and there is no freedom of expansion. Hence, a CTE mismatch between the silicon and metal defines the stress behavior. Copper has a CTE almost ten times larger than silicon, therefore during thermal variation it will apply significant pressure to the silicon in order to expand, leading to higher stress in comparison to the unfilled TSVs. Alternatively, tungsten is very thermally compatible with silicon (low CTE mismatch), diminishing the TSVs’ mechanical influence on the surroundings. In summary, the stress induced in silicon by unfilled TSVs is mainly determined by the geometry of the hole, while for filled TSVs the mechanical properties of the metal also play a considerable role in determining the stress levels.