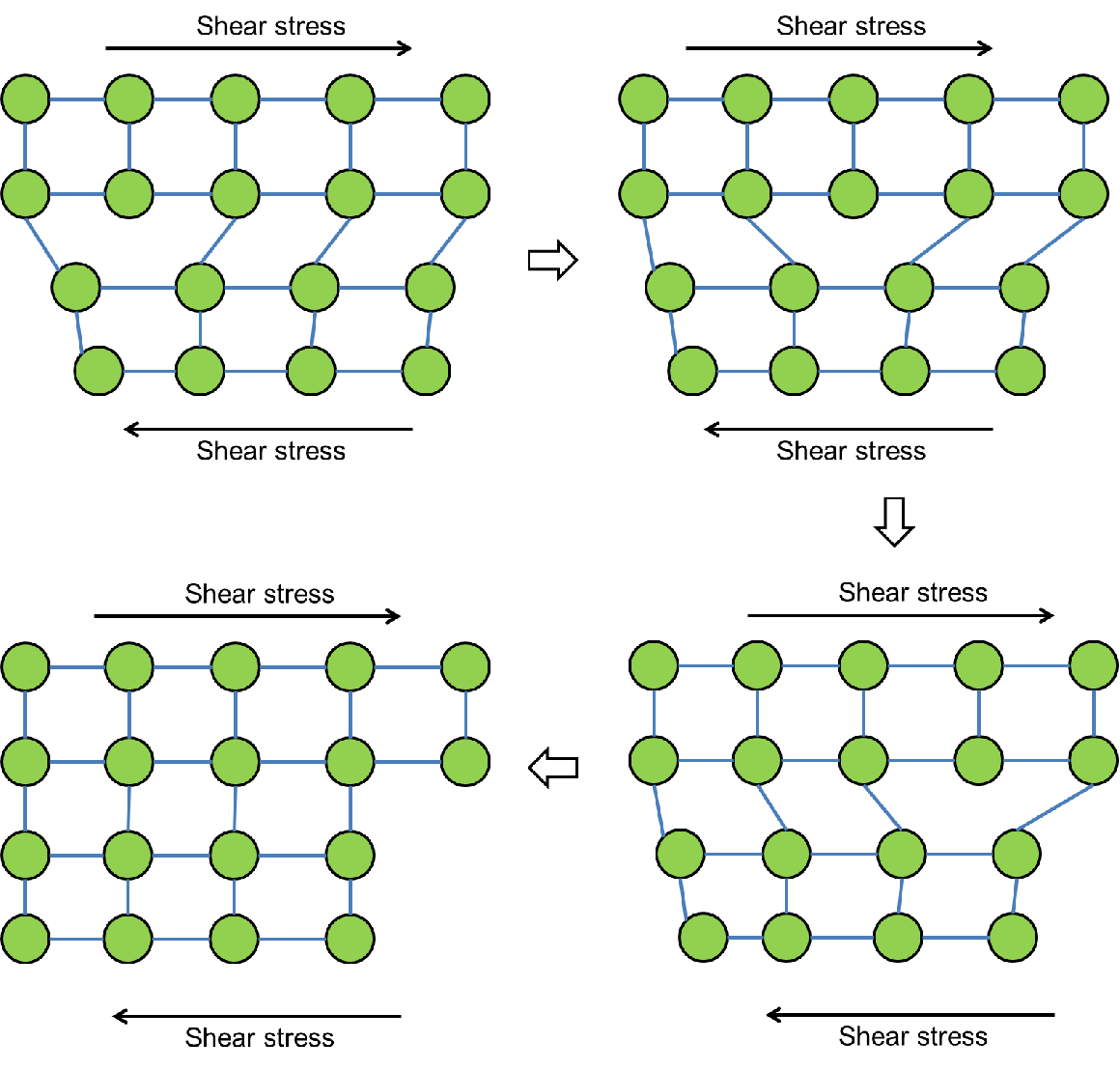
| Figure 5.17.: | Dislocation propagation inside a film crystal. |
During film deposition, different stress sources pressure the material atoms to conform to the substrate and to their environmental conditions. Consequently, the film sustains a strained state and small deformations, also called dislocations, arise in the crystal structure of the deposited material [91]. Dislocations manifest themselves in two forms: edge dislocation and screw dislocation [91]. However, a mix of both types is the most common observation in materials.
Dislocations can propagate through the film due to the actions of an external disturbance. This movement, when sustained, relaxes the film and constitutes one of the main mechanisms of strain relaxation of materials. A fair example of such a phenomenon can be described by considering Fig. 5.17. A dislocation movement is characterized by the breaking of an atomic bond around the defect, followed by a different bond formation. For a system in equilibrium, such processes occur in a random fashion. However, when the system is disturbed by an external force, the crystal lattice deforms elastically, which favors the dislocation propagation in a preferred direction. If the force persists for sufficient time, the defect propagates to the material surface, where boundary effects take place and part of the strained energy inside the film is released. Consequently, the film experiences a reduced strained state and a reduction in the intrinsic stress.
The continuous propagation of the dislocations depends on several conditions and properties inside the material. As shown in Fig. 5.18, the dislocation moves along the indicated slip plane, following the slip direction [92]. Such slip systems are not available for every plane inside the crystal, but are instead determined by the symmetries of the lattice. Usually, slip planes are defined by the lattice with the highest atom density (closed package configuration) and the slip direction is defined by the shortest distance between atoms on the slip plane [91]. Naturally, the external force must favor the movement of a dislocation in a slip system, otherwise a continuous propagation is very unlikely.
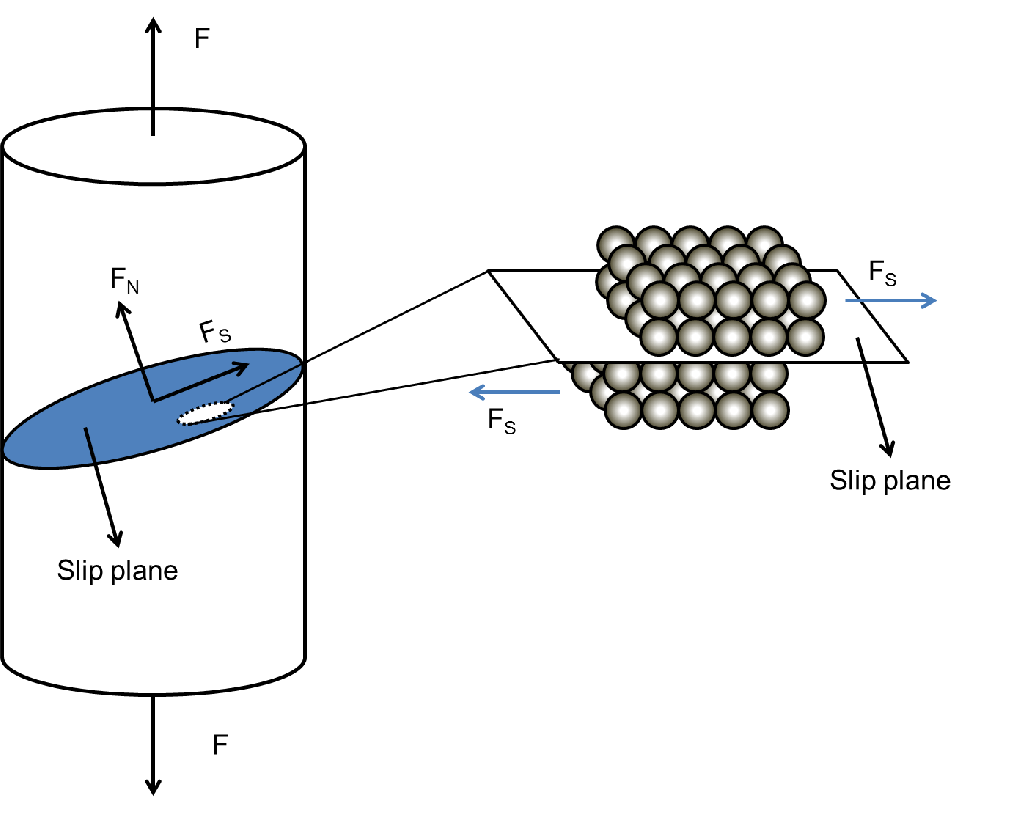
| Figure 5.18.: | Slip system inside a material. A force parallel to the slip plane must exist in order to activate the dislocations movement. |
The dynamic of dislocation glide is not governed solely by the slip system and the external force. Dislocations interact with each other and with grain boundaries during motion. Moreover, the propagation is a kinetic process and temperature effects can not be neglected. In the case of polycrystalline materials, each grain has its own slip system which should be accounted for. All these conditions make the modeling of the dislocation glide a challenging task. Actually, there is a variety of models available, which consider dislocation propagation under different conditions [92]. In general, however, they can be divided into low and high temperature models. The concept of low temperature in this case depends on the melting point of the material. Any temperature below approximately 10% of the material’s melting point is usually considered low [92]. This work is limited to the model named after Freund for low temperature dislocation glide with obstacles [92], which is usually a suitable choice for metals present in microelectronic metals’ structures[93].
The dislocation movement is by definition a plastic process, since the material changes its structure permanently. As in every plastic process the amount of deformation will depend on the amount of time during which a material must withstand a stress state. Moreover, the deformation is accumulated over time, which means that in order to predict the plastic deformation of an eventual load, the previous amount of plastic deformation should be known in advance. Unfortunately, this information is rarely available. Therefore, it is more convenient to describe plastic deformations by means of their rate over time. This rate is known as strain-rate, which is defined in the model of low temperature dislocation glide with obstacles by
![[ ( ) ]
ΔF-- σs-
˙γ = γ0exp − kT 1− ˆτ ,](diss443x.png) | (5.3) |
where 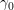 is a pre-exponential factor assumed to be constant for high values of
is a pre-exponential factor assumed to be constant for high values of
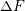 , k is the Boltzmann constant, T is the temperature, and
, k is the Boltzmann constant, T is the temperature, and 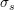 is the shear
stress over the material. The symbol
is the shear
stress over the material. The symbol 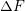 represents the activation energy of an
obstacle and it defines the energy needed for the dislocation to overcome a single
obstacle without an external force. Lastly, the property
represents the activation energy of an
obstacle and it defines the energy needed for the dislocation to overcome a single
obstacle without an external force. Lastly, the property 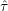 describes the amount of
shear stress required to trigger the dislocation glide without aid from the thermal
energy.
describes the amount of
shear stress required to trigger the dislocation glide without aid from the thermal
energy.