5.4.2  Strain Relaxation Driven by Temperature

Temperature variation is one the most common stress sources in metal films of semiconductor devices, especially during processing. Devices are baked several times in thermal cycles which can reach up to 500C. In such situations, an understanding of the stress evolution in metal films is mandatory to create mechanically stable TSVs.

During thermal variation every deformation (elastic or plastic) in the film is the result of thermal expansion (or contraction) as described by

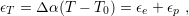(5.4)

where 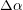stands for the CTE mismatch between the film and substrate, 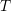is the temperature during a thermal cycle, 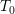is the initial temperature, and the indexes T, e, and p refer to thermal, elastic, and plastic strain, respectively. The stress can be related to the strain by Hooke’s law as described in Section 2.2.1. However, the film is a 2D system so the relation can be simplified. Additionally, as mentioned in the scallop problem of Section 5.2, an equibiaxial assumption in thin films’ analyses is quite common. Hence, the problem dimension can still be further reduced to 1D and Hooke’s relation for thin films can be described by

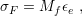(5.5)

where 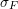is the stress in the film and 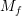is known as the biaxial modulus. In order to compute the effects of thermal variation on the stress, 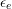in (5.5) must be replaced by (5.4) as in

For reasons stated in the previous section, it is convenient to describe plastic deformations by means of the time derivative. In principle, the same approach could be applied to (5.6), but for the particular case of thermal variation, an analysis of (5.6) by derivatives of temperature is of greater interest, as in [93]

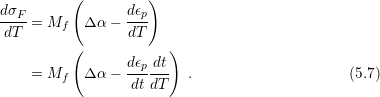
Substituting (5.3) in (5.7) one obtains the final relation:

(5.8)

where the shear stress 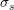relates to the equibiaxial stress by the Schmid factor () as in .
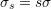