6.3.1 Hoffman’s Model
Hoffman was the first to acknowledge the energy balance of the coalescence stress formation
[104]. He realized that adjacent islands snap together, in order to minimize the free surface
energy at the cost of an increased elastic energy. He claimed that the zipping process
(islands merging) takes place, when the distance between the islands reach a critical
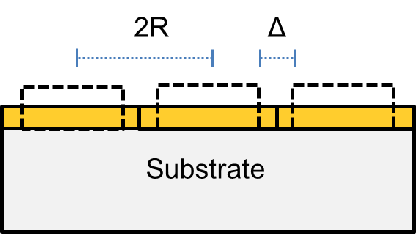
distance ( ). Nix reviewed Hoffman’s work and added a simplified geometry model as
depicted in Fig. 6.5.
). Nix reviewed Hoffman’s work and added a simplified geometry model as
depicted in Fig. 6.5.
Nix restated Hoffman’s theory by looking into the energy balance of two islands before and
after impingement [105]. Before impingement, the system free energy is given
by
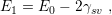 | (6.1) |
where 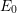 is the free surface energy per unit area of the top surface of the film and
the substrate/film interface, and
is the free surface energy per unit area of the top surface of the film and
the substrate/film interface, and 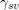 is the free surface energy per unit area of
the islands’ lateral surfaces. After islands merge the system free energy is given
by
is the free surface energy per unit area of
the islands’ lateral surfaces. After islands merge the system free energy is given
by
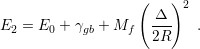 | (6.2) |
Before island impingement there are two independent surfaces, one for each island, with an
amount of energy per surface area of 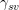 . After impingement part of the surfaces energy
(
. After impingement part of the surfaces energy
(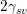 ) is exerted for the formation of the interface between them (grain boundary). This
energy amount per unit area is represented by
) is exerted for the formation of the interface between them (grain boundary). This
energy amount per unit area is represented by 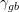 . The remainder of the surface
free energy is converted by the islands’ stretching with elastic energy, which is
represented by the second term of (6.2). Actually, this is just the conservation of the free
energy (
. The remainder of the surface
free energy is converted by the islands’ stretching with elastic energy, which is
represented by the second term of (6.2). Actually, this is just the conservation of the free
energy (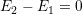 ), which can be used to calculate
), which can be used to calculate 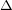 . The resulting
. The resulting 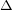 is
is
![[ ]1∕2
1−-ν-
Δ = 4R (2γsv − γgb) E .](diss498x.png) | (6.3) |
The coalescence stress can then be computed from Hooke’s law using 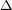 as in
as in
![( ) [ ]1∕2
Δ 2γsv − γgb
σ = Mf 2R- = Mf ---2R----- .](diss500x.png) | (6.4) |
Hoffman’s model overestimates the coalescence stress in the film, mainly because of the
simple geometry assumed for the islands. However, it is a reasonable approach for low
adatom materials. Moreover, it is a simple model when compared to the alternatives
and it can be useful as a quick estimate of the upper bound of the coalescence
stress.
 ). Nix reviewed Hoffman’s work and added a simplified geometry model as
depicted in Fig. 6.5.
). Nix reviewed Hoffman’s work and added a simplified geometry model as
depicted in Fig. 6.5.
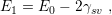
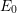 is the free surface energy per unit area of the top surface of the film and
the substrate/film interface, and
is the free surface energy per unit area of the top surface of the film and
the substrate/film interface, and 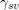 is the free surface energy per unit area of
the islands’ lateral surfaces. After islands merge the system free energy is given
by
is the free surface energy per unit area of
the islands’ lateral surfaces. After islands merge the system free energy is given
by
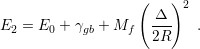
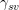 . After impingement part of the surfaces energy
(
. After impingement part of the surfaces energy
(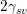 ) is exerted for the formation of the interface between them (grain boundary). This
energy amount per unit area is represented by
) is exerted for the formation of the interface between them (grain boundary). This
energy amount per unit area is represented by 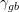 . The remainder of the surface
free energy is converted by the islands’ stretching with elastic energy, which is
represented by the second term of (
. The remainder of the surface
free energy is converted by the islands’ stretching with elastic energy, which is
represented by the second term of (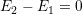 ), which can be used to calculate
), which can be used to calculate 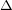 . The resulting
. The resulting 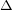 is
is
![[ ]1∕2
1−-ν-
Δ = 4R (2γsv − γgb) E .](diss498x.png)
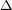 as in
as in
![( ) [ ]1∕2
Δ 2γsv − γgb
σ = Mf 2R- = Mf ---2R----- .](diss500x.png)