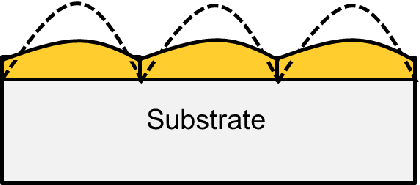
| Figure 6.6.: | Nix-clemens model. |
Nix and Clemens employed a different geometry for describing the droplets [105]. They considered islands with an elliptical shape which coalesces to form a cycloid shape surface as depicted in Fig. 6.6.
Instead of a critical distance (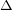 ), there is a critical height (
), there is a critical height (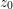 ) in Nix’s and Clemens’
approach. It defines the extension of the interface between the two islands.
) in Nix’s and Clemens’
approach. It defines the extension of the interface between the two islands.
In addition to the island shape, Nix and Clemens adopted a different view of the problem.
They treated each cusp of the cycloid surface as a crack and developed their model based on
this assumption. Their main argument was that the amount of the energy which must be
supplied to grow the crack further (strain energy release rate) must be equal to the amount
of energy left after boundary formation (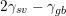 ). Their idea can be neatly summarized
by
). Their idea can be neatly summarized
by
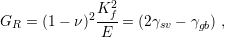 | (6.5) |
where 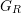 is the strain energy release rate and
is the strain energy release rate and 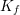 is the stress intensity factor which is
used as a parameter to estimate the stress around a cracked tip. Nix and Clemens used
is the stress intensity factor which is
used as a parameter to estimate the stress around a cracked tip. Nix and Clemens used
 from the results of Cheng-Hsin’s and Huajian’s work regarding cycloid
surfaces [106]. Hence, (6.5) can be further developed and the average film stress is given
by
from the results of Cheng-Hsin’s and Huajian’s work regarding cycloid
surfaces [106]. Hence, (6.5) can be further developed and the average film stress is given
by
![[ ]
1+ ν 2γsv − γgb 1∕2
σ = 1−--νE ---2R----- .](diss508x.png) | (6.6) |
The Nix-Clemens model also overestimates the stress, but it is based on a more realistic geometry. The criticism of Nix-Clemens’ model lies in the loose description of the zipping process. It was assumed by Nix and Clemens that the average stress is linearly dependent on the average strain. However, island coalescence is not an instantaneous process and the problem configuration, as well as the average stress, changes during the zipping process. In such cases the assumptions made by Nix and Clemens would be invalid.