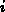 als Änderung des Realteils des Stroms des Kontakts
als Änderung des Realteils des Stroms des Kontakts 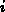 bei
Änderung der einzelnen Kontaktspannungen berechnen (unter der Annahme, daß
die Wechselspannung
bei
Änderung der einzelnen Kontaktspannungen berechnen (unter der Annahme, daß
die Wechselspannung 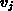 keinen Imaginärteil aufweist):
keinen Imaginärteil aufweist):




Mit MINIMOS ist es möglich, neben statischer und transienter Analyse auch
eine Kleinsignalanalyse durchzuführen. Dabei werden die
Halbleitergleichungen an einem berechneten Arbeitspunkt linearisiert und
diese linearen Gleichungen gelöst. Damit lassen sich Leitwerte eines
Kontakts 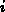 als Änderung des Realteils des Stroms des Kontakts
als Änderung des Realteils des Stroms des Kontakts 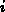 bei
Änderung der einzelnen Kontaktspannungen berechnen (unter der Annahme, daß
die Wechselspannung
bei
Änderung der einzelnen Kontaktspannungen berechnen (unter der Annahme, daß
die Wechselspannung 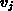 keinen Imaginärteil aufweist):
keinen Imaginärteil aufweist):
Ebenso ergeben sich die Kapazitäten als die Änderungen der Imaginärteile der Ströme nach den einzelnen Spannungen:
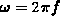 bezeichnet die Kreisfrequenz.
bezeichnet die Kreisfrequenz.
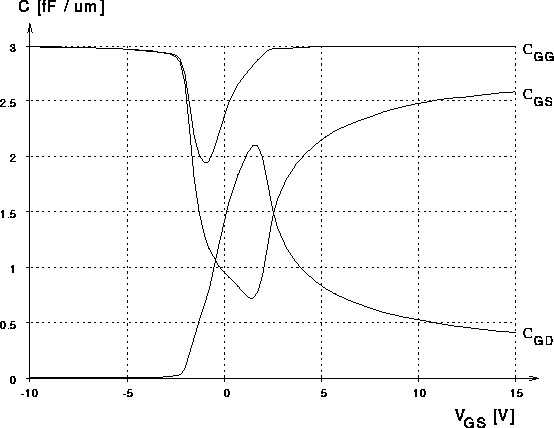
Abbildung 5.37: Numerische Simulation der
Eingangskapazität und ihrer Aufteilung in Source- und Drainanteile für
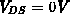 .
.
In Abb. 5.37 ist das Ergebnis der numerischen Simulation der
Eingangskapazität (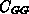 ) der auch für die statischen Simulationen
verwendeten DMOS-Struktur zu sehen. Es ist außerdem die Aufteilung der
Eingangskapazität in Source (
) der auch für die statischen Simulationen
verwendeten DMOS-Struktur zu sehen. Es ist außerdem die Aufteilung der
Eingangskapazität in Source (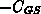 ) und Drain (
) und Drain (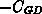 )
zuzurechnenden Teilen dargestellt (es muß für alle Kontakte
)
zuzurechnenden Teilen dargestellt (es muß für alle Kontakte 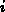
gelten). Diese Simulationen wurden bei einer Frequenz von 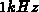 durchgeführt. Bei dieser Frequenz ist mit quasistatischem Verhalten zu
rechnen (die Ladungen können den Spannungsänderungen uneingeschränkt
folgen). Da bei DMOS-Transistoren nur eine Ladungsträgerart am
Stromtransport beteiligt ist, ist ihre Schaltgeschwindigkeit (im Vergleich
zu Leistungsbipolartransistoren) i.a. so hoch, daß man immer von
quasistatischen Betrachtungen ausgehen kann (zumal es sich um
Leistungs- und nicht Hochfrequenzanwendungen handelt).
durchgeführt. Bei dieser Frequenz ist mit quasistatischem Verhalten zu
rechnen (die Ladungen können den Spannungsänderungen uneingeschränkt
folgen). Da bei DMOS-Transistoren nur eine Ladungsträgerart am
Stromtransport beteiligt ist, ist ihre Schaltgeschwindigkeit (im Vergleich
zu Leistungsbipolartransistoren) i.a. so hoch, daß man immer von
quasistatischen Betrachtungen ausgehen kann (zumal es sich um
Leistungs- und nicht Hochfrequenzanwendungen handelt).
Der Verlauf der Kapazitätskurven kann folgendermaßen erklärt werden:
Für geringe Gatespannungen (kleiner ca. 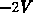 ) ergibt sich als
Eingangskapazität annähernd die Oxidkapazität. Der Kanal befindet sich in
Akkumulation, das Driftgebiet an seiner Grenze zum Gateoxid in Inversion.
Die Gate-Drain-Kapazität ist verschwindend klein, da die Inversionsladung
an der Grenze Driftzone-Gateoxid einerseits von der mit der Inversionsschicht
verbundenen Raumladungszone vom Drainkontakt abgeschirmt wird, und
andererseits diese Inversionsladung über die Akkumulationsladung im
Kanalbereich eine sehr gut leitende Verbindung zum Sourcekontakt hat.
Die Sourcekapazität ist damit fast gleich groß wie die
Eingangskapazität. Bei einer Gatespannung von etwa
) ergibt sich als
Eingangskapazität annähernd die Oxidkapazität. Der Kanal befindet sich in
Akkumulation, das Driftgebiet an seiner Grenze zum Gateoxid in Inversion.
Die Gate-Drain-Kapazität ist verschwindend klein, da die Inversionsladung
an der Grenze Driftzone-Gateoxid einerseits von der mit der Inversionsschicht
verbundenen Raumladungszone vom Drainkontakt abgeschirmt wird, und
andererseits diese Inversionsladung über die Akkumulationsladung im
Kanalbereich eine sehr gut leitende Verbindung zum Sourcekontakt hat.
Die Sourcekapazität ist damit fast gleich groß wie die
Eingangskapazität. Bei einer Gatespannung von etwa 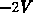 erreicht
man die ,,Einsatzspannung der Driftzone``, mit anderen Worten: Die Inversion
an der Grenze Driftzone-Gateoxid geht in Verarmung über (vgl. Verlauf
der Eingangskapazität eines
erreicht
man die ,,Einsatzspannung der Driftzone``, mit anderen Worten: Die Inversion
an der Grenze Driftzone-Gateoxid geht in Verarmung über (vgl. Verlauf
der Eingangskapazität eines 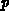 -Kanal MOSFETs). Bei dieser Gatespannung
befindet sich das Kanalgebiet noch immer in Akkumulation. Die
Gesamtkapazität nimmt ab, ebenso natürlich auch die
Gate-Source-Kapazität. Die Abnahme letzterer ist aber noch wesentlich
größer, da sich die Kapazität Gate-Oxid-Depletionszone an der
Driftzonengrenzfläche dem
Drainkontakt (vgl. die Zuordnung der Verarmungskapazität zum Bulkkontakt
in einem klassischen MOSFET) zuordnen läßt. Damit steigt die
Gate-Drain-Kapazität etwas an. Ab ca.
-Kanal MOSFETs). Bei dieser Gatespannung
befindet sich das Kanalgebiet noch immer in Akkumulation. Die
Gesamtkapazität nimmt ab, ebenso natürlich auch die
Gate-Source-Kapazität. Die Abnahme letzterer ist aber noch wesentlich
größer, da sich die Kapazität Gate-Oxid-Depletionszone an der
Driftzonengrenzfläche dem
Drainkontakt (vgl. die Zuordnung der Verarmungskapazität zum Bulkkontakt
in einem klassischen MOSFET) zuordnen läßt. Damit steigt die
Gate-Drain-Kapazität etwas an. Ab ca. 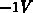 Gatespannung nimmt die
gesamte Eingangskapazität wieder zu. Das Gebiet an der Grenze
Driftzone-Gateoxid geht in Akkumulation über. Die Gate-Drain-Kapazität
steigt an, da die Kapazität der Akkumulationsschicht im Regime unterhalb der
Einsatzspannung des Transistors (diese liegt bei etwas über
Gatespannung nimmt die
gesamte Eingangskapazität wieder zu. Das Gebiet an der Grenze
Driftzone-Gateoxid geht in Akkumulation über. Die Gate-Drain-Kapazität
steigt an, da die Kapazität der Akkumulationsschicht im Regime unterhalb der
Einsatzspannung des Transistors (diese liegt bei etwas über 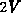 ) dem
Drainkontakt zuzuordnen ist, es gibt ja noch keine leitende Verbindung zum
Sourcekontakt hin. Im Gebiet unterhalb der Schwellspannung (von ca.
) dem
Drainkontakt zuzuordnen ist, es gibt ja noch keine leitende Verbindung zum
Sourcekontakt hin. Im Gebiet unterhalb der Schwellspannung (von ca. 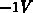 bis ca.
bis ca. 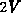 ) wird die Gate-Source-Kapazität von der Kanalkapazität
bestimmt. In diesem Bereich geht das Kanalgebiet (von Akkumulation) in
Verarmung und bei der Schwellspannung in Inversion über. Oberhalb der
Schwellspannung des DMOS-Transistors nähert sich die
Eingangskapazität wieder der Oxidkapazität an. Die Aufteilung in zum
Source- bzw. Drainkontakt gehörige Anteile wird durch das sich
verändernde Widerstandsverhältnis zwischen Kanal auf der einen
Seite und dem Epi-Widerstand auf der anderen
Seite bestimmt. Oberhalb der Einsatzspannung beginnt der Kanal, mit
zunehmender Gatespannung seinen Widerstand im Vergleich zu dem des
Driftgebiets wesentlich zu verringern, und damit steigt die
Gate-Source-Kapazität, die Gate-Drain-Kapazität sinkt wieder.
) wird die Gate-Source-Kapazität von der Kanalkapazität
bestimmt. In diesem Bereich geht das Kanalgebiet (von Akkumulation) in
Verarmung und bei der Schwellspannung in Inversion über. Oberhalb der
Schwellspannung des DMOS-Transistors nähert sich die
Eingangskapazität wieder der Oxidkapazität an. Die Aufteilung in zum
Source- bzw. Drainkontakt gehörige Anteile wird durch das sich
verändernde Widerstandsverhältnis zwischen Kanal auf der einen
Seite und dem Epi-Widerstand auf der anderen
Seite bestimmt. Oberhalb der Einsatzspannung beginnt der Kanal, mit
zunehmender Gatespannung seinen Widerstand im Vergleich zu dem des
Driftgebiets wesentlich zu verringern, und damit steigt die
Gate-Source-Kapazität, die Gate-Drain-Kapazität sinkt wieder.
Sehr interessant ist der Verlauf der Kapazitäten für höhere
Drainspannungen. Die Abbildungen 5.38 bis 5.40 zeigen die
Ergebnisse numerischer Simulationen mit MINIMOS für die Kapazitäten
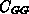 ,
, 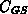 und
und 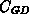 bei Drainspannungen von
bei Drainspannungen von 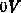 bis
bis 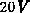 .
.
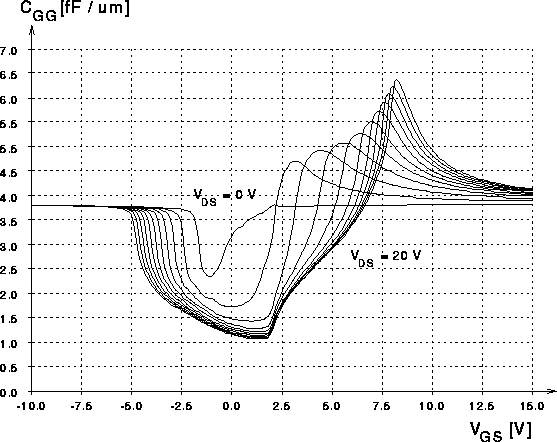
Abbildung 5.38: Numerische Simulation von 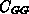 fuer
fuer 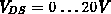 .
.
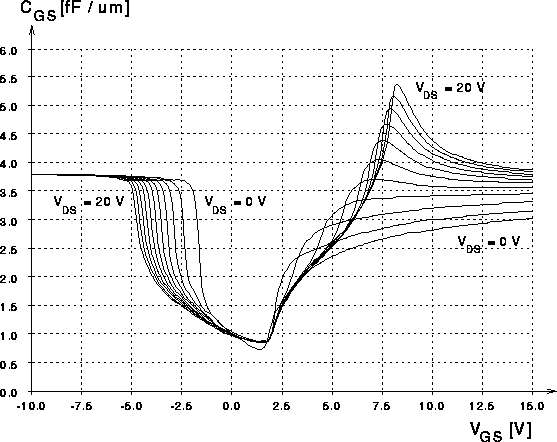
Abbildung 5.39: Numerische Simulation von 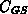 fuer
fuer 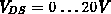 .
.
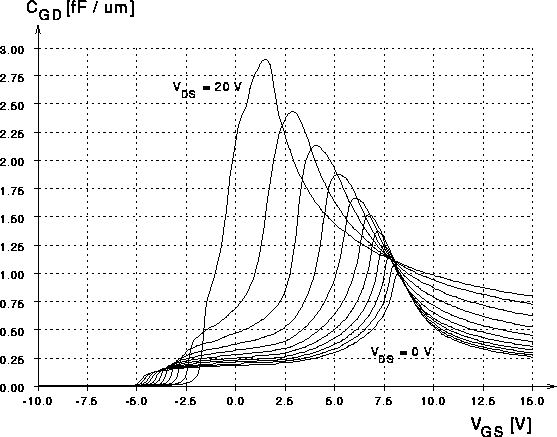
Abbildung 5.40: Numerische Simulation von 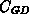 fuer
fuer 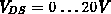 .
.
Betrachtet man die Kurvenverläufe von negativen zu positiven
Gatespannungen, so ist zuerst auffällig, daß das Absinken der Eingangs-
und der Gate-Source-Kapazität für höhere Drainspannungen
bei negativeren Gatespannungen einsetzt. Wie oben bereits erwähnt, wird
dieses Absinken durch die ,,Einsatzspannung der Driftzone`` bedingt, also
den Übergang von Inversion zu Verarmung an der Grenzfläche
Driftzone-Gateoxid. Man kann nun die Driftzone mit den Kanalgebieten zweier
benachbarter DMOS-Zellen, dem sich über das gesamte Driftgebiet
erstreckenden Gateoxid und dem darüberliegenden Gatekontakt als 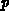 -Kanal
MOSFET (mit sehr langem Kanal)
betrachten. Für einen
-Kanal
MOSFET (mit sehr langem Kanal)
betrachten. Für einen 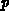 -Kanal MOSFET verschiebt sich die Einsatzspannung
mit positiven Bulkspannungen (entspricht dem Drainkontakt in einem
DMOS-Transistor) zu negativeren Spannungen hin. Dies ist der hinreichend
bekannte ,,Body-Effekt``, welcher die Schwellspannung mit
-Kanal MOSFET verschiebt sich die Einsatzspannung
mit positiven Bulkspannungen (entspricht dem Drainkontakt in einem
DMOS-Transistor) zu negativeren Spannungen hin. Dies ist der hinreichend
bekannte ,,Body-Effekt``, welcher die Schwellspannung mit 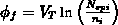 entsprechend [6]
(auf den DMOS-Transistor umgelegt) um
entsprechend [6]
(auf den DMOS-Transistor umgelegt) um
verschiebt. Als zweiter wesentlicher Effekt zeigt sich bei Erhöhung der
Drainspannung in einem DMOS-Transistor, daß die Eingangskapazität erst bei
wesentlich höheren Gatespannungen wieder ansteigt. Da dieser Effekt
ebenfalls mit der Kapazität an der Grenzfläche Driftzone-Gateoxid
zusammenhängt, kann dies wieder am besten durch Betrachtung eines 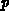 -Kanal
MOSFETs erklärt werden. Der Übergang vom Bereich der Verarmung zu dem der
Akkumulation erfolgt bei der sog. Flachbandspannung. Dies ist jene Spannung,
bei der die Bandverbiegung an der Grenzfläche Silizium-Gateoxid
verschwindet. Liegt keine Spannung am Gate (im Vergleich zum Bulk in einem
MOSFET) an, ist die Bandverbiegung wegen der unterschiedlichen
Austrittsarbeiten von Silizium und Gatematerial und zufolge Ladungen im Oxid
von Null verschieden. Die Flachbandspannung wird im wesentlichen bei
heutigen MOS-Technologien von der Austrittsarbeitsdifferenz bestimmt
[6], welche für einen
-Kanal
MOSFETs erklärt werden. Der Übergang vom Bereich der Verarmung zu dem der
Akkumulation erfolgt bei der sog. Flachbandspannung. Dies ist jene Spannung,
bei der die Bandverbiegung an der Grenzfläche Silizium-Gateoxid
verschwindet. Liegt keine Spannung am Gate (im Vergleich zum Bulk in einem
MOSFET) an, ist die Bandverbiegung wegen der unterschiedlichen
Austrittsarbeiten von Silizium und Gatematerial und zufolge Ladungen im Oxid
von Null verschieden. Die Flachbandspannung wird im wesentlichen bei
heutigen MOS-Technologien von der Austrittsarbeitsdifferenz bestimmt
[6], welche für einen 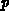 -Kanal MOSFET mit degeneriertem,
-Kanal MOSFET mit degeneriertem,
 -dotiertem Polysilizium als Gatematerial negativ ist. Legt man die
Verhältnisse auf die DMOS-Struktur um, so gilt für die Flachbandbedingung
(für
-dotiertem Polysilizium als Gatematerial negativ ist. Legt man die
Verhältnisse auf die DMOS-Struktur um, so gilt für die Flachbandbedingung
(für 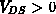 und
und 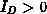 ):
):
Es ergibt sich z.B. für eine Drainspannung von 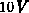 der Übergang
Verarmung-Akkumulation bei ca.
der Übergang
Verarmung-Akkumulation bei ca. 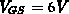 und jener bei
und jener bei 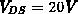 bei ca.
bei ca. 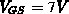 (siehe Abb. 5.39). Der Einfluß des Terms
(siehe Abb. 5.39). Der Einfluß des Terms
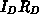 ist nicht vernachlässigbar (der Widerstand des JFET-Gebiets ist
in
ist nicht vernachlässigbar (der Widerstand des JFET-Gebiets ist
in 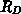 enthalten).
enthalten).
Der Anstieg der Gate-Drain-Kapazität (bei vom Inversionsregime an der
Grenze Driftzone-Gateoxid ausgehend steigender Gatespannung) verschiebt sich
natürlich auch entsprechend der durch den Bulkeffekt negativeren
,,Einsatzspannung der Driftzone``. Mit dem sog. body-Faktor 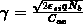 ergibt sich für die
Verarmungsladung im Gebiet der Depletion (zwischen der Einsatzspannung und
der Flachbandspannung) für eine MOS-Kapazität mit
ergibt sich für die
Verarmungsladung im Gebiet der Depletion (zwischen der Einsatzspannung und
der Flachbandspannung) für eine MOS-Kapazität mit 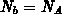 (
(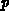 -Substrat, vgl. Gleichung 6.106)
-Substrat, vgl. Gleichung 6.106) 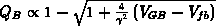 . Wendet man dies
auf die DMOS-Struktur an, so erhält man (mit
. Wendet man dies
auf die DMOS-Struktur an, so erhält man (mit 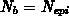 ) für den
Bereich der Verarmung der Grenzfläche Driftzone-Gateoxid:
) für den
Bereich der Verarmung der Grenzfläche Driftzone-Gateoxid:
Der tatsächliche Kurvenverlauf weicht von dieser idealen Beziehung ab. Grund dafür ist der Einfluß des Kanals, der in der Depletion der Driftzonen-Grenzschicht zum Gateoxid sehr wesentlich ist.
Besonders interessant sind die Verläufe der Eingangs- und der Gate-Source-Kapazität oberhalb der Einsatzspannung. Beide zeigen mit einsetzender Akkumulation an der Grenze Driftzone-Gateoxid eine stark ausgeprägte Überhöhung. Diese beeinflußt das Schaltverhalten des DMOS-Transistors wesentlich. Sie tritt lediglich bei höheren Drain-Source-Spannungen auf.
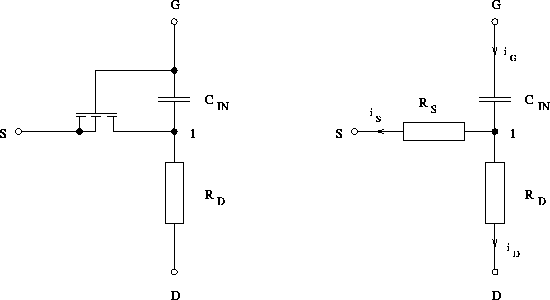
Abbildung 5.41: Ersatzschaltbilder zur Erklärung des
Miller-Effekts.
Grund dafür sind die nicht vernachlässigbaren Widerstände zwischen
Source und der Grenze Driftzone-Gateoxid bzw. besonders zwischen Drain und
dieser Grenzfläche, die zufolge des bekannten Millereffekts [80]
zu dieser Erhöhung führen. Das linke Ersatzschaltbild in Abb. 5.41
zeigt den Kanal, die Eingangskapazität und den Drainwiderstand. Die
Eingangskapazität ist zur Vereinfachung lediglich als Gate-Drain-Kapazität
des Kanaltransistors angenommen. Dies kann aber leicht durch den großen
flächenmäßigen Anteil der Überlappungszone des Gatekontakts über dem
Driftgebiet zwischen benachbarten DMOS-Zellen gerechtfertigt werden. Im
AC-Fall sind alle DC-Spannungsquellen kurzzuschließen. Am Knoten  tritt nun wegen des Drainwiderstands ein Potential von
tritt nun wegen des Drainwiderstands ein Potential von 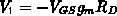 auf. Damit fällt über der Eingangskapazität
auf. Damit fällt über der Eingangskapazität 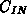 eine Spannung
von
eine Spannung
von 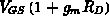 ab. Mit diesem Faktor wird die
Eingangskapazität verstärkt, es kommt zu einer Überhöhung über die
Oxidkapazität [121].
ab. Mit diesem Faktor wird die
Eingangskapazität verstärkt, es kommt zu einer Überhöhung über die
Oxidkapazität [121].
Die Eingangskapazität teilt sich nun in einen dem Source zuzurechnenden
und einen dem Drain zuzuschlagenden Anteil auf. Die nochmals vereinfachte
Darstellung rechts in Abb. 5.41 dient als Ausgangspunkt für eine
einfache Abschätzung zur Aufteilung von 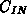 (hier ist der
JFET-Widerstand wieder in
(hier ist der
JFET-Widerstand wieder in 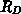 enthalten):
enthalten):
Für genügend kleine Frequenzen (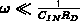 ,
,
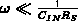 ) kann man noch Abschätzungen für
) kann man noch Abschätzungen für
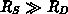
und für 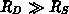
treffen.
Dies erklärt den Verlauf der Kurven in den Abbildungen 5.39
und 5.40. Die Überhöhung der Eingangskapazität teilt sich also
entsprechend den Widerständen zu Source und Drain hin auf. Da der
Drainwiderstand aufgrund der Stromsättigung mit steigender Drainspannung im
Vergleich mit dem Widerstand zum Sourcekontakt wesentlich größer
wird, kommt die Überhöhung hauptsächlich bei 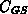 zum Tragen.
zum Tragen.



