Next: 4.2.4 Specific Heat Up: 4.2 Lattice and Thermal Previous: 4.2.2 Mass Density Contents
The thermal conductivity is modeled by a power law:
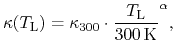 |
For AlN the variation of the measured values for the thermal conductivity is
smaller (Fig. 4.2). We assume
![]() =350 W/mK, which is
close to the value reported in [299]. The parameter
=350 W/mK, which is
close to the value reported in [299]. The parameter ![]() , which
models the decrease with temperature, is calibrated against measured data
[299,300,301].
, which
models the decrease with temperature, is calibrated against measured data
[299,300,301].
As of today no studies of the temperature dependent thermal conductivity of InN
are available. Based on [302] a
![]() =176 W/mK at 300 K
is assumed. This is a theoretical estimation, while the measured value was only
45 W/mK due to phonon scattering by point-defects and grain-boundaries.
=176 W/mK at 300 K
is assumed. This is a theoretical estimation, while the measured value was only
45 W/mK due to phonon scattering by point-defects and grain-boundaries.
Several expressions exist for the thermal conductivity
![]() of semiconductor alloys. As an example, Adachi et al. [303] use
one based on Abeles's complex model [304]. However, an even more
straightforward approach is proposed in [305], where a harmonic
mean is used to model the conductivity at 300 K, while the exponent
of semiconductor alloys. As an example, Adachi et al. [303] use
one based on Abeles's complex model [304]. However, an even more
straightforward approach is proposed in [305], where a harmonic
mean is used to model the conductivity at 300 K, while the exponent
![]() is linearly interpolated as there is no experimental data for
temperatures other than 300 K yet:
is linearly interpolated as there is no experimental data for
temperatures other than 300 K yet:
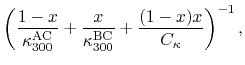 |
|||
For In![]() Ga
Ga![]() N
N ![]() =1.5 W/mK is adopted, again matching
the model in [303] (Fig. 4.4) and the
experimental data of Pantha et al. [307]. For
In
=1.5 W/mK is adopted, again matching
the model in [303] (Fig. 4.4) and the
experimental data of Pantha et al. [307]. For
In![]() Al
Al![]() N a fit to the only available experimental data
[308] resulted in an
N a fit to the only available experimental data
[308] resulted in an ![]() =1.2 W/mK
(Fig. 4.5).
=1.2 W/mK
(Fig. 4.5).