Next: 4.3 Band Structure Up: 4.2 Lattice and Thermal Previous: 4.2.3 Thermal Conductivity Contents
The lattice specific heat
![]() is modeled by the following expression proposed in [305]:
is modeled by the following expression proposed in [305]:
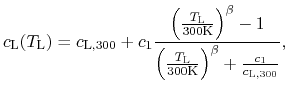 |
where
![]() is the value of the specific heat at 300 K and
is the value of the specific heat at 300 K and
![]() and
and ![]() are fitting parameters. Fig. 4.6 shows a
comparison between the calibrated model (values are listed in
Table 4.5) and measurements as a function of temperature for
GaN. The results both of Kremer et al. [309] and
Danilchenko et al. [310] are from bulk wurtzite GaN
while most previous measurements were conducted on polycrystalline
powder samples. Our model is calibrated against the model of Danilchenko
et al., which is in excellent agreement with their own
measurements for the heat capacity in the 0 K
are fitting parameters. Fig. 4.6 shows a
comparison between the calibrated model (values are listed in
Table 4.5) and measurements as a function of temperature for
GaN. The results both of Kremer et al. [309] and
Danilchenko et al. [310] are from bulk wurtzite GaN
while most previous measurements were conducted on polycrystalline
powder samples. Our model is calibrated against the model of Danilchenko
et al., which is in excellent agreement with their own
measurements for the heat capacity in the 0 K![]() 300 K range and also
with experimental results given in [309].
300 K range and also
with experimental results given in [309].
The parameter values for AlN are based on the summarized results in [138].
For the heat capacity of InN several works are based on the experimental data provided by Krukowski et al. [302]. Their results are shown in Fig. 4.7 together with the models of Leitner et al. [311] and Zieborak et al. [312], which both provide models based on measurement results. In the present work the model is calibrated against the data in [311].
The specific heat coefficients for alloy materials are expressed by a linear interpolation between the values of the binary materials [305]: