4.3.2 Band Gap Energy Offset

An energy offset ( $\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}$) is used to align the valence band of different materials. In this work GaN is chosen as the reference for the III-V materials ( $\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}=0$ eV). The energies of the conduction and valence band edges are calculated by

$$\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{v}}}} = \ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}$$

$$\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{c}}}} = \ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{v}}}}+ \ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}$$

The valence-band-offset of AlN $\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}^\ensuremath{\mathrm{AlN}}$ is chosen as 1.12 eV, which is equal to 40% of the total band gap discontinuity as reported by Westmeyer et al. [333] obtained from a measurement of the linewidth of the excitonic transition in an Al$_{0.18}$Ga$_{0.82}$N alloy. This value is larger than the previously reported 0.7 eV as in [334] obtained by x-ray photoemission spectroscopy. However, it is closer to the intrinsic value as it is free from effects introduced by interface defects and inhomogeneities.

The most widely cited value for the valence band offset of InN/GaN is the one reported by Martin et al. [334] ( $\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}^\ensuremath{\mathrm{InN}}=1.05$ eV). It was however determined over a decade ago, and the recent reevaluation of the band structure have rendered it dated. Recent studies show a valence band offset between 0.58 [335] and 0.62 eV [323]. The band alignment is shown schematically in Fig. 4.9.

Figure 4.9: Band alignment of InN, GaN, and AlN at room temperature.

For alloys the offset energy is calculated by the following expression [138]:

$$\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}... ...{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}^\ensuremath{\mathrm{BC}}},$$

where $\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}^\ensuremath{\mathrm{AC}}$ and $\ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{off}}}}^\ensuremath{\mathrm{BC}}$ are the offset energies for the binary materials.

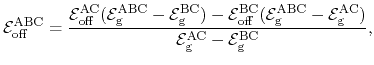As an example, for Al$_{x}$Ga$_{1-x}$N with $x$=0.22 the valence-band-offset against GaN is 0.25 eV. Our setup provides a value of 0.225 eV for $x$=0.2, which is in a good agreement with the experimentally determined offset of 0.25 eV [336] for the same composition.