4.5 Spontaneous and Piezoelectric Polarization

A good understanding of the electrical polarization effects at the material interfaces is key to proper device simulation. III-V nitrides are the only III-V materials that show spontaneous polarization $P_\ensuremath{\mathrm{SP}}$. This has been found to increase from GaN over InN to AlN [172] and it also has a negative sign. The reason is an intrinsic asymmetry of the bonding in the equilibrium wurtzite crystal structure. However, mechanical stress also results in polarization, which is then called piezoelectric polarization $P_\ensuremath{\mathrm{PZ}}$. It is negative for tensile and positive for compressive strained AlGaN layers. Therefore, the orientation of the spontaneous and piezoelectric polarization is parallel in case of tensile strain and antiparallel in case of compressive strain. AlGaN layers grown on GaN buffers are always under tensile strain, thus only this case will be further discussed. As both polarizations have the same direction the total polarization is simply the sum:

$$P = P_\ensuremath{\mathrm{PZ}} + P_\ensuremath{\mathrm{SP}}.$$

Further, the total polarization of the AlGaN layer is stronger than that of the underlying relaxed GaN buffer layer. The negative spontaneous polarization of both layers and the negative piezoelectric polarization vector under tensile strain points from the Nitrogen atom towards the nearest Gallium atom along the [0001] axis. Thus, for Ga-faced polarity crystals the total polarization is directed towards the substrate, while for N-faced crystals it is directed towards the surface. It is found that the polarization-induced sheet charge is positive for AlGaN on top of GaN with Ga-face polarity and GaN on top of AlGaN with N-face polarity.

In the following the polarization induced charge at an AlGaN/GaN interface is calculated. Using the provided parameters and the same approach, the polarization for different material interfaces can be determined accordingly.

The spontaneous polarization $P_\ensuremath{\mathrm{SP}}$ at the AlGaN/GaN interface is calculated by [358]:

$$P_\ensuremath{\mathrm{SP}}=P_\ensuremath{\mathrm{SP,AlN}}+P_\ensuremath{\mathrm{SP,GaN}}(1-x),$$

Table 4.13: Spontaneous polarization parameters [C/m$^{2}$].

	GaN	AlN	InN	Refs.
P $\ensuremath{\mathrm{SP}}$	-0.029	-0.081	-0.032	[172]
P $\ensuremath{\mathrm{SP}}$	-0.034	-0.090	-0.042	[359]

The piezoelectric polarization $P_\ensuremath{\mathrm{PZ}}$ is calculated by:

$$P_\ensuremath{\mathrm{PZ}}=2 \cdot \frac{a-a_0}{a_0} \left( e_{31} - e_{33} \cdot \frac{C_{13}}{C_{33}} \right),$$

without taking partial relaxation into account. The parameters $a$ and $a_0$ are the lattice constants, $e_{13}$ and $e_{33}$ are the piezoelectric coefficients, and $C_{13}$ and $C_{33}$ denote the elastic constants. The parameter values for both the spontaneous (Table 4.13) and piezoelectric (Table 4.14) polarization are achieved by the revised calculations of [359].

Table 4.14: Piezoelectric polarization parameters.

Material	$a$	$a_0$	$e_{13}$	$e_{33}$	$C_{13}$	$C_{33}$
	[Å]	[Å]	[C/m$^{2}$]	[C/m$^{2}$]	[GPa]	[GPa]
GaN	3.197	5.210	-0.37	0.67	68	354
AlN	3.108	4.983	-0.62	1.50	94	377
InN	4.580	5.792	-0.45	0.81	70	205

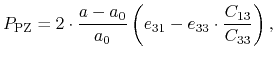Using the provided method and the listed values, the polarization induced charges for AlGaN/GaN, InAlN/GaN, and InGaN/GaN interfaces are calculated and shown in Fig. 4.20. While using slightly different values than Ambacher et al. [358], we still obtain a good agreement with their results. Furthermore, the significantly larger charges at the InAlN/GaN interface must be noted (due to the higher spontaneous polarization in AlN).

The dependence of the spontaneous polarization coefficients for GaN, AlN, and InN on temperature has been measured to be minimal [360,361]. There are no reports on the temperature dependence of the piezoelectric polarization.

Figure 4.20: Piezoelectric and spontaneous polarization-induced charge $\sigma /\mathrm {q}(P_\ensuremath {\mathrm {SP}}+P_\ensuremath {\mathrm {PE}})$.