3.1.1 Notation

  In this analysis a  single-electron circuit consists of  branches (capacitors, tunnel junctions, voltage sources, and current sources) that start and end at  nodes. The electrical description of a circuit consists of all node potentials, node charges, and branch currents. Usually only a part of the node potentials, node charges, and branch currents are known. The unknown voltages, charges and currents have to be calculated from Kirchhoff's laws. In order to distinguish between the various kinds of nodes, we define the following terms. If the potential of a node is given it is called a   potential-node. This is the case for a node that is connected to a grounded voltage source (see node 1 in Fig. 3.1), since the voltage source defines the potential of the node.

  

Figure 3.1: Nodes are distinguished in potential-nodes, charge-nodes, and floating-nodes, because before the circuit analysis different quantities are known for different nodes. For potential-nodes the node potential and for charge-nodes the node charge is known. Floating-nodes have to be treated differently in the circuit analysis, since neither charge nor potential are known a priori.

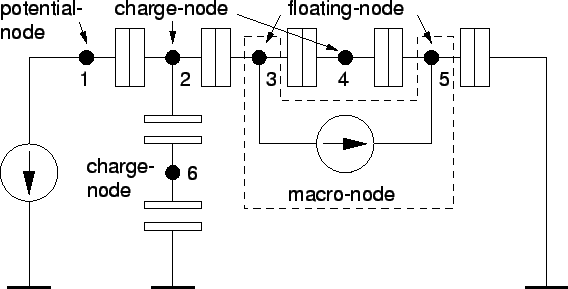   Charge-nodes are nodes with known charge and are either nodes with a constant charge, or nodes which charge can change by an integer number of the elementary charge. A charge-node has a constant charge if it is connected to capacitors only, since no charge can enter or exit, such as node 6. If a charge-node is connected to at least one tunnel junction it can change its charge by an integer number of the elementary charge due to electrons tunneling onto and off the node. Not grounded voltage sources that are not connected to other grounded voltage sources produce   floating-nodes. A priori neither charge nor potential is known of such nodes. However, the potential differences of all floating-nodes in a   macro-node are known. For example the potential difference between nodes 3 and 5 in Fig. 3.1 is determined by a voltage source. In addition to the known potential differences of floating-nodes comprising a macro-node, the charge of the macro-node is known. The charge of the macro-node is the sum of the charges of its floating-nodes. For a macro-node consisting of N_f floating-nodes, N_f-1 potential differences and one charge, the sum of the floating-node charges, are known. These are enough equations to determine with the other node charges and potentials the missing quantities of the floating-nodes. The charge of a macro-node can be treated equally to a charge on a charge-node, since the macro-node charge can also only change by an integer number of the elementary charge.

Altogether, a network consists of N+1 nodes, where N_c nodes are charge-nodes, N_p nodes are potential-nodes, N_f nodes are floating-nodes ( N=N_p+N_f+N_c), and one node is the ground-node. In general, subscripts p, f, and c denote potential-node, floating-node, and charge-node quantities, respectively. Matrices are written as bold upper case letters. For instance the capacitance matrix is denoted by C. The unit matrix is I. Vectors are bold lower case letters, such as the charge vector q, and are always column vectors. A row vector is written as transposed column vector q^T.