A.4 Capacitance of an Arbitrary Arrangement of Spheres

  It is possible with the same method, as was used before for calculating the capacitance of two spheres, to calculate the capacitance of an arbitrary arrangement of not intersecting conducting spheres with different diameters and an optional infinite conducting plane.

One starts with a charge on the sphere for which the total capacitance is to be obtained. Then compensation charges are placed in all other spheres, so that these spheres stay zero equipotential surfaces. In case an infinite conducting plane is present, all charges so far calculated have to be mirrored on this plane to make it a zero equipotential (see Fig. A.5).

  

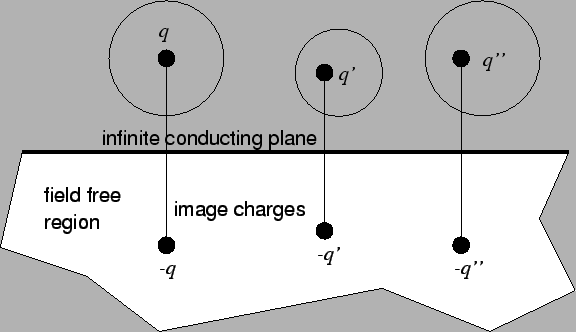
Figure A.5: In order to make the infinite plane a zero equipotential, all charges have to be mirrored.

But every placed compensation charge will disturb the before compensated potentials. Hence, the compensation charges have to be recursively compensated themselves. For more than two conductors the number of compensation charges grows exponentially for every level of recursion. For N spheres the number of charges progresses as
$$\begin{gather}1\rightarrow (N-1)\rightarrow (N-1)^2\rightarrow (N-1)^3\rightarrow\ldots \end{gather}$$
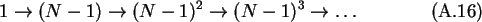
In order to assure convergence of the successive approximation the magnitudes of compensation charges have to decrease sufficiently. A sufficient but not mandatory condition that the sum of compensation charges which are added with each level of recursion vanishes is 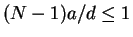$(N-1)a/d \leq 1$, where again a is the radius and d the center to center distance of spheres. For spheres with equal diameters the ratio a/d is less than 1/2, which assures that the algorithm always converges for two and three spheres. In the case of more spheres usually not all spheres will be close to each other, which means that the ratio a/d is in average much smaller than 1/2, and hence the algorithm converges for arrangements with more conductors. For example, lines of an arbitrary number of spheres are successfully calculated. The results are shown in Table A.2. However if too many spheres are placed too closely together the algorithm does not converge. No simple convergence criteria exists. A possibility to detect lack of convergence is to monitor the sum of added compensation charges. If the sum grows with each iteration the algorithm will not converge.

 

Table: Capacitances of spheres aligned in a line. 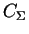$C\protect_{\protect\Sigma}$ is the total capacitance of the center sphere which has the number 1, C₁₀ is its self-capacitance and the C_1i are the capacitances between the center sphere and spheres next in line. All spheres have a diameter of 2 nm and a distance from surface to surface of 1 nm to their neighbors. The surrounding medium has $\protect\epsilon\protect_r = 1$. 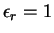All capacitances are given in aF.

sphere arrangement	$C_{\Sigma }$	C10	C12	C13
	0.111	0.111
	0.128	0.0843	0.0433
	0.142	0.0612	0.0403
	0.143	0.0520	0.0375	0.00788