Next: C Solutions to Schrödinger's
Up: Dissertation Christoph Wasshuber
Previous: A.4 Capacitance of an
B Fermi Energy Dependence on Free Charge Carrier Concentration
The number of allowed k-values per unit volume of k-space in a piece of
material with volume V is 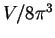 .
The number of energy levels in the
Fermi sphere, considering two spin values for each k-value, is
.
The number of energy levels in the
Fermi sphere, considering two spin values for each k-value, is

Thus if there are N electrons in a volume V the concentration is
n = N/V, which leads to
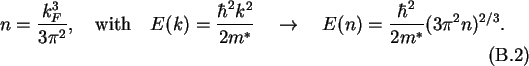
In the case of semiconductors the band gap has to be taken into account.
Using the Boltzmann approximation to the
Fermi distribution the carrier
concentrations in the conduction and valence band are
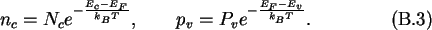
Noting that for the intrinsic case,
EF = EF,i,
nc=pv=ni the
concentrations may be written as
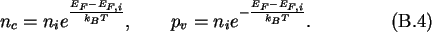
And with the net carrier concentration n=nc-pv one derives
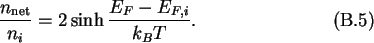
Christoph Wasshuber