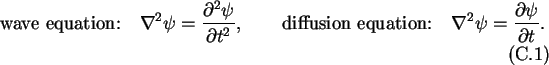Next: C.1 The Infinite Potential
Up: Dissertation Christoph Wasshuber
Previous: B Fermi Energy Dependence
The time-dependent Schrödinger wave equation which describes the motion
of a particle under the influence of a potential, reads
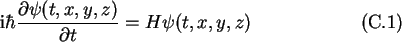
We are interested in the motion of a particle in a potential landscape.
Thus the Hamilton operator is replaced with the Hamilton operator for the
free electron plus the potential function describing the potential landscape.
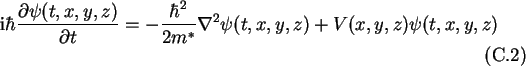
It should be noted that the time-dependent Schrödinger wave equation is,
in fact, a `diffusion' not a `wave' equation, the time derivative, being of
the first and not of the second order. A wave equation and a diffusion
equation have the form
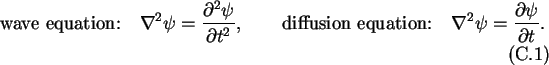
Thus indeed the Schrödinger equation (C.2) has the form
of a diffusion equation. With the separation Ansatz
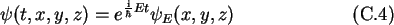
one derives the time-invariant one-dimensional Schrödinger equation
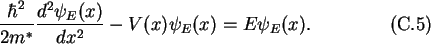
For an easier notation in the following examples, 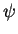 stands for
stands for
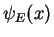 .
.
Christoph Wasshuber