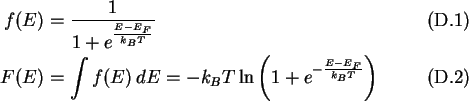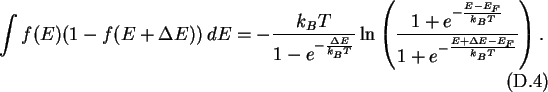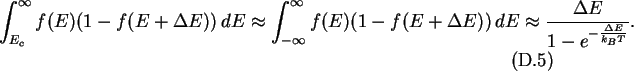


Next: E Fermi's Golden Rule
Up: Dissertation Christoph Wasshuber
Previous: C.3 The Rectangular Potential
D Integration of Fermi Functions
The Fermi function and its antiderivative is given by
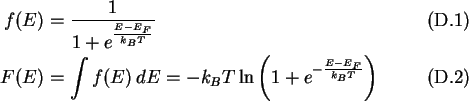
The product
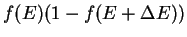 can be written as
can be written as
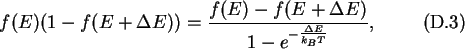
and the corresponding antiderivative is
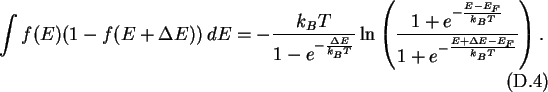
A usual approximation for
metal tunnel
junctions, where the Fermi energy
is much bigger than the conduction band edge,
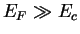 ,
is to set
,
is to set
 ,
thus
,
thus
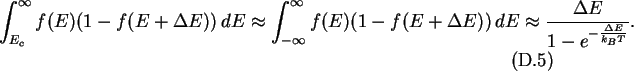
Christoph Wasshuber